
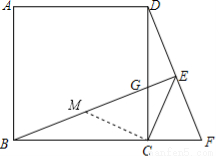
在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
(1)若正方形ABCD边长为3,DF=4,求CG的长;
(2)求证:EF+EG= CE.
CE.

(1) 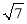 ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据正方形的性质可得∠BCG=∠DCB=∠DCF=90°,BC=DC,再根据同角的余角相等求出∠CBG=∠CDF,然后利用“角边角”证明△CBG和△CDF全等,根据全等三角形对应边相等可得BG=DF,再利用勾股定理列式计算即可得解;
(2)过点过点C作CM⊥CE交BE于点M,根据全等三角形对应边相等可得CG=CF,全等三角形对应角相等可得∠F=∠CGB,再利用同角的余角相等求出∠MCG=∠ECF,然后利用“角边角”证明△MCG和△ECF全等,根据全等三角形对应边相等可得MG=EF,CM=CE,从而判断出△CME是等腰直角三角形,再根据等腰直角三角形的性质证明即可.
试题解析:(1)【解析】
∵四边形ABCD是正方形,
∴∠BCG=∠DCB=∠DCF=90°,BC=DC,
∵BE⊥DF,
∴∠CBG+∠F=∠CDF+∠F,
∴∠CBG=∠CDF,
在△CBG和△CDF中,
 ,
,
∴△CBG≌△CDF(ASA),
∴BG=DF=4,
∴在Rt△BCG中,CG2+BC2=BG2,
∴CG=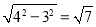 ;
;
(2)证明:如图,过点C作CM⊥CE交BE于点M,
∵△CBG≌△CDF,
∴CG=CF,∠F=∠CGB,
∵∠MCG+∠DCE=∠ECF+∠DCE=90°,
∴∠MCG=∠ECF,
在△MCG和△ECF中,
 ,
,
∴△MCG≌△ECF(SAS),
∴MG=EF,CM=CE,
∴△CME是等腰直角三角形,
∴ME=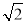 CE,
CE,
又∵ME=MG+EG=EF+EG,
∴EF+EG=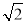 CE.
CE.
考点:1.正方形的性质;2.全等三角形的判定与性质;3.勾股定理;4.等腰直角三角形.


科目:初中数学 来源:2015届黑龙江省八年级下学期期末考试数学试卷(解析版) 题型:填空题
已知菱形的两条对角线长分别为2cm,3cm,则它的面积是 _________ cm2.
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:选择题
用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第13个“口”字需用棋子颗数为( )
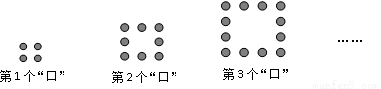
A.52 B.50 C.48 D.46
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:选择题
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简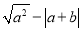 的结果为( )
的结果为( )

A.2a+b B.-2a+b C.b D.2a-b
查看答案和解析>>
科目:初中数学 来源:2015届重庆市八年级下期期末考试数学试卷(解析版) 题型:选择题
如图,矩形ABCD中,E、G为AB、CD边上的点,F为BC的中点,且BE=1,CG=4,BC=4,EF⊥FG,则EG的长为( )
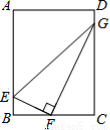
A.5 B.10 C.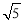 D.
D.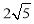
查看答案和解析>>
科目:初中数学 来源:2015届辽宁省北票市八年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,△ABC中,AD为∠BAC的平分线,AD的垂直平分线EF交BC的延长线于点F,连接AF.求证:∠B=∠CAF.
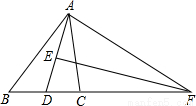
查看答案和解析>>
科目:初中数学 来源:2015届辽宁省丹东市八年级下学期期中考试数学试卷(解析版) 题型:选择题
下列变形,是因式分解的是( )
A.x(x-1)=x2-x B.x2-x+1 = x(x-1)+1
C.x2-x = x(x-1) D.2a(b+c)=2ab+2ac
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com