
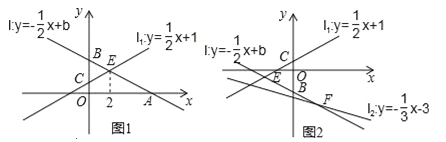
����Ŀ����ͼ����ֱ֪��l��y=��![]() x+b��x�ᡢy��ֱ��ڵ�A��B��ֱ��l1��y=
x+b��x�ᡢy��ֱ��ڵ�A��B��ֱ��l1��y=![]() x+1��y�ύ�ڵ�C����ֱ��l��ֱ��l1�Ľ���ΪE
x+1��y�ύ�ڵ�C����ֱ��l��ֱ��l1�Ľ���ΪE
��1����ͼ1������E�ĺ�����Ϊ2�����A�����ꣻ
��2���ڣ�1����ǰ���£�D��a��0��Ϊx���ϵ�һ�㣬����D��x��Ĵ��ߣ��ֱ�ֱ��l��ֱ��l1�ڵ�M��N�����Ե�B��C��M��NΪ������ı���Ϊƽ���ı��Σ���a��ֵ��
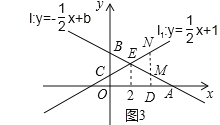
��3����ͼ2����ֱ��l��ֱ��l2��y=��![]() x��3�Ľ���ΪF�����Ƿ���ڵ�B��ʹBE=BF�������ڣ����ֱ��l�Ľ���ʽ���������ڣ���˵�����ɣ�
x��3�Ľ���ΪF�����Ƿ���ڵ�B��ʹBE=BF�������ڣ����ֱ��l�Ľ���ʽ���������ڣ���˵�����ɣ�
���𰸡���1����A������Ϊ��6��0����
��2�����Ե�B��C��M��NΪ������ı���Ϊƽ���ı��Σ�a��ֵΪ4��
��3�����ڵ�B��ʹBE=BF����ʱֱ��l�Ľ���ʽΪy=��![]() x��
x��![]() ��
��
�������������������1���ɵ�E�ĺ�������һ�κ���ͼ���ϵ���������������ҳ���E�����꣬�����ô���ϵ�����������ֱ��![]() �Ľ���ʽ����
�Ľ���ʽ����![]() ���
���![]() ��ֵ�����ɵó���A�����ꣻ
��ֵ�����ɵó���A�����ꣻ
��2�����ݵ�D�ĺ�����Ϊa����һ�κ���ͼ���ϵ���������������ҳ���M��N�����꣬�Ӷ��ó��߶�MN�ij��ȣ��ֱ���ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() �����
�����![]() �����꣬�ٸ���ƽ���ı��ε����ʼ��ɵó�����a�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
�����꣬�ٸ���ƽ���ı��ε����ʼ��ɵó�����a�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��3��������ڣ�����ֱ��![]() �Ľ���ʽ�ɷ����飬�ⷽ���������E�����꣬����ֱ��
�Ľ���ʽ�ɷ����飬�ⷽ���������E�����꣬����ֱ��![]() �Ľ���ʽ�ɷ����飬�ⷽ���������F�����꣬���
�Ľ���ʽ�ɷ����飬�ⷽ���������F�����꣬���![]() ���ɵó�����b��һԪһ�η��̣��ⷽ�����bֵ������ý⣮
���ɵó�����b��һԪһ�η��̣��ⷽ�����bֵ������ý⣮
���������(1)�ߵ�E��ֱ��l1�ϣ��ҵ�E�ĺ�����Ϊ2��
���E������Ϊ(2,2)��
�ߵ�E��ֱ��l�ϣ�
![]() ��ã�b=3��
��ã�b=3��
��ֱ��l�Ľ���ʽΪ![]()
��y=0ʱ,��![]()
��ã�x=6,
���A������Ϊ(6,0).
(2)�������⻭��ͼ�Σ���ͼ3��ʾ,
��x=aʱ��![]()
![]()
��x=0ʱ,![]()
��BC=31=2.
��BC��MN��
�൱MN=BC=2ʱ���Ե�B. C.M��NΪ������ı���Ϊƽ���ı��Σ�
��ʱ|a2|=2��
��ã�a=4��a=0(��ȥ).
�൱�Ե�B. C.M��NΪ������ı���Ϊƽ���ı��Σ�a��ֵΪ4.
(3)�������.
����ֱ��l��l1�Ľ���ʽ�ɷ�����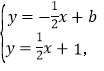
��ã�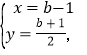
���E������Ϊ![]()
����ֱ��l��l2�Ľ���ʽ�ɷ���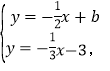
��ã�![]()
���F������Ϊ(18+6b,92b).
��BE=BF����E.F����ֱ��l�ϣ�
��b1=186b,��ã�![]()
��ʱֱ��l�Ľ���ʽΪ![]()
�ʴ��ڵ�B,ʹBE=BF,��ʱֱ��l�Ľ���ʽΪ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ABCD�У�E��CD����һ�㣬
��1������ADE�Ƶ�A��˳ʱ�뷽����ת��ʹAD��AB�غϣ��õ���ABF����ͼ1��ʾ���۲��֪����DE��ȵ��߶����� ������AFB=���� ��
��2����ͼ2��������ABCD�У�P��Q�ֱ���BC��CD���ϵĵ㣬�ҡ�PAQ=45������ͨ����ת�ķ�ʽ˵����DQ+BP=PQ��
��3���ڣ�2�����У�����BD�ֱ�AP��AQ��M��N���㻹������ת��˼��˵��BM2+DN2=MN2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ����(����)
A. a2+a2��2a4B. a2a3��a6
C. a3��a3��aD. (��ab2)2��a2b4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��CDΪ��O��ֱ������EOD=60�㣬AE����O�ڵ�B��E����AB=OC����(1)��A�Ķ�����(2)��AEO����.
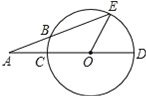
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��Ϊ����У������ijУ�ƻ���һ�鳤Ϊ60�ף���Ϊ40�ij����οյ�����һ�������λ��ԣ����������������µĿյ�����ͬ������ͨ������ͨ����Ϊ![]() ��.
��.
��1�����Ե����Ϊ____![]() ���ú�
���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2�����ͨ����ռ��������������οյ������![]() �������ʱͨ���Ŀ���
�������ʱͨ���Ŀ���
��3����֪ij�ֹ�˾��ͨ�������Ե����![]() ��Ԫ����
��Ԫ����![]() ��Ԫ���������
��Ԫ���������![]()
![]() ֮��ĺ�����ϵ��ͼ2��ʾ�����ѧУ�����ɸù�˾�н�����Ŀ����Ҫ������ͨ���Ŀ��Ȳ�����2���Ҳ�����10�ף���ôͨ����Ϊ����ʱ������ͨ���ͻ��Ե������Ϊ105920Ԫ
֮��ĺ�����ϵ��ͼ2��ʾ�����ѧУ�����ɸù�˾�н�����Ŀ����Ҫ������ͨ���Ŀ��Ȳ�����2���Ҳ�����10�ף���ôͨ����Ϊ����ʱ������ͨ���ͻ��Ե������Ϊ105920Ԫ

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com