
【题目】阅读材料,解答问题:如果一个四位自然数,十位数字是千位数字的2倍与百位数字的差,个位数字是千位数字的2倍与百位数字的和,则我们称这个四位数“依赖数”,例如,自然数2135,其中3=2×2﹣1,5=2×2+1,所以2135是“依赖数”.
(1)请直接写出最小的四位依赖数;
(2)若四位依赖数的后三位表示的数减去百位数字的3倍得到的结果除以7余3,这样的数叫做“特色数”,求所有特色数.
(3)已知一个大于1的正整数m可以分解成m=pq+n4的形式(p≤q,n≤b,p,q,n均为正整数),在m的所有表示结果中,当nq﹣np取得最小时,称“m=pq+n4”是m的“最小分解”,此时规定:F(m)=![]() ,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=
,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=![]() =1,求所有“特色数”的F(m)的最大值.
=1,求所有“特色数”的F(m)的最大值.
【答案】(1)1022;(2)3066,2226;(3)![]()
【解析】
(1)由于千位不能为0,最小只能取1;根据题目得出相应的公式:十位=2×千位﹣百位,个位=2×千位+百位,分别求出十位和个位,即可求出最小的四位依赖数;
(2)设千位数字是x,百位数字是y,根据“依赖数”定义,则有:十位数字是(2x﹣y),个位数字是(2x+y),依据题意列出代数式然后表示为7的倍数加余数形式,然后求出x、y即可,从而求出所有特色数;
(3)根据最小分解的定义可知: n越小,p、q越接近,nq﹣np才越小,才是最小分解,此时F(m)=![]() ,故将(2)中特色数分解,找到最小分解,然后将n、p、q的值代入F(m)=
,故将(2)中特色数分解,找到最小分解,然后将n、p、q的值代入F(m)=![]() ,再比较大小即可.
,再比较大小即可.
解:(1)由题意可知:千位一定是1,百位取0,十位上的数字为:2×1-0=2,个位上的数字为:2×1+0=2则最小的四位依赖数是1022;
(2)设千位数字是x,百位数字是y,根据“依赖数”定义,
则有:十位数字是(2x﹣y),个位数字是(2x+y),
根据题意得:100y+10(2x﹣y)+2x+y﹣3y=88y+22x=21(4y+x)+(4y+x),
∵21(4y+x)+(4y+x)被7除余3,
∴4y+x=3+7k,(k是非负整数)
∴此方程的一位整数解为:x=4,y=5(此时2x+y>10,故舍去);x=3,y=7(此时2x﹣y<0,故舍去);x=3,y=0;x=2,y=2;x=1,y=4(此时2x﹣y<0,故舍去);
∴特色数是3066,2226.
(3)根据最小分解的定义可知: n越小,p、q越接近,nq﹣np才越小,才是最小分解,此时F(m)=![]() ,
,
由(2)可知:特色数有3066和2226两个,
对于3066=613×5+14=61×50+24
∵1×613-1×5>2×61-2×50,
∴3066取最小分解时:n=2,p=50,q=61
∴F(3066)=![]()
对于2226=89×25+14=65×34+24,
∵1×89-1×25>2×65-2×34,
∴2226取最小分解时:n=2,p=34,q=65
∴F(2226)=![]()
∵![]()
故所有“特色数”的F(m)的最大值为:![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C是AB的中点,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x秒(x>0).
(1)当x= 秒时,点P到达点A;
(2)运动过程中点P表示的数是 (用含x的代数式表示);
(3)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第6个图形的小圆个数是( )

A. 56 B. 54 C. 44 D. 42
查看答案和解析>>
科目:初中数学 来源: 题型:
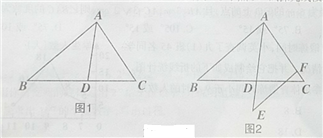
【题目】已知,如图1,AD是△ABC的角平分线,且AD=BD,
(1)求证:△CDA∽△CAB;
(2)若AD=6,CD=5,求AC的值;
(3)如图2,延长AD至E,使AE=AB,过E点作EF∥AB,交AC于点F,试探究线段EF
与线段AD的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
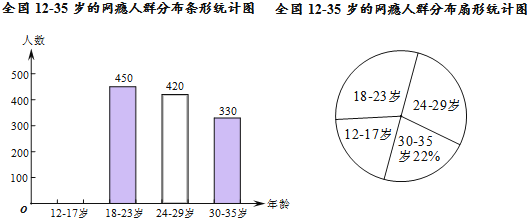
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人,并请补全条形统计图;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是 度;
(3)据报道,目前我国12﹣35岁“网瘾人数”约为2000万,请估计其中12﹣17岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
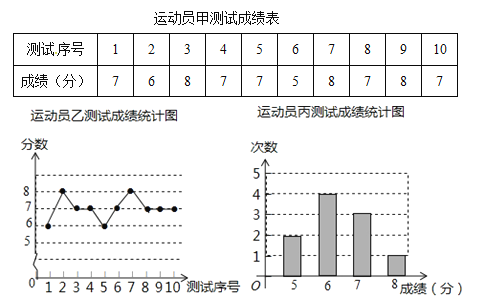
(1)写出运动员甲测试成绩的众数为_________;运动员乙测试成绩的中位数为_________;运动员丙测试成绩的平均数为_________;
(2)经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是( )
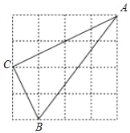
A. AB=5 B. ∠C=90° C. AC=2![]() D. ∠A=30°
D. ∠A=30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有( )千米到达甲地.
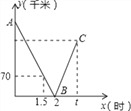
A. 70 B. 80 C. 90 D. 100
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com