练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在4×4的正方形网格中，△ABC的顶点都在格点上，下列结论错误的是（　　）

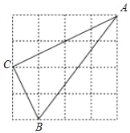
    A. AB＝5 B. ∠C＝90° C. AC＝2 D. ∠A＝30°

    【答案】D

    【解析】

    首先根据每个小正方形的边长为1，结合勾股定理求出AB、AC、BC的长，进而判断A、C的正误；再判断较短的两边的平方和与较长边的平方是否相等，进而可判断B的正误；在上步提示的基础上，判断BC与AB是否存在二倍关系，进而即可判断D的正误.

    ∵每个小正方形的边长为1，

    根据勾股定理可得：AB＝5，AC＝2，BC＝.

    故A、C正确；

    ∵2＋(2)2＝52，

    ∴△ABC是直角三角形，

    ∴∠C＝90°.

    故B正确；

    ∵∠C＝90°，AC＝2BC，而非AB＝2BC，

    ∴∠A≠30°.

    故D错误.

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】观察下列两个等式：，，给出定义如下：我们称使等式 成立的一对有理数，为“共生有理数对”，记为（，），如：数对（，），（，），都是“共生有理数对”．

    （1）数对（，），（，）中是“共生有理数对”吗？说明理由．

    （2）若（，）是“共生有理数对”，则（，）是“共生有理数对”吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料，解答问题：如果一个四位自然数，十位数字是千位数字的2倍与百位数字的差，个位数字是千位数字的2倍与百位数字的和，则我们称这个四位数“依赖数”，例如，自然数2135，其中3＝2×2﹣1，5＝2×2+1，所以2135是“依赖数”．

    （1）请直接写出最小的四位依赖数；

    （2）若四位依赖数的后三位表示的数减去百位数字的3倍得到的结果除以7余3，这样的数叫做“特色数”，求所有特色数．

    （3）已知一个大于1的正整数m可以分解成m＝pq+n4的形式（p≤q，n≤b，p，q，n均为正整数），在m的所有表示结果中，当nq﹣np取得最小时，称“m＝pq+n4”是m的“最小分解”，此时规定：F（m）＝，例：20＝1×4+24＝2×2+24＝1×19+14，因为1×19﹣1×1＞2×4﹣2×1＞2×2﹣2×2，所以F（20）＝＝1，求所有“特色数”的F（m）的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

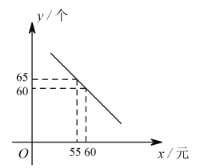
    【题目】某体育用品商店试销一款成本为 50 元的排球，规定试销期间单价不低于成本价，且获利不得高于 40%。经试销发现，销售量 （个）与销售单价 （元）之间满足如图所示的一次函数关系.

    （1）试确定与 之间的函数关系式；

    （2）若该体育用品商店试销的这款排球所获得的利润为 元，试写出利润 （元）与销售单价 （元）之间的函数关系式；当试销单价定为多少元时，该商店可获最大利润？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，点分别是上的中点，连接并延长至点，使，连接.

    （1）证明：；

    （2）若，AC=2，连接BF，求BF的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

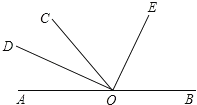
    【题目】如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°．

    （1）写出图中小于平角的角．

    （2）求出∠BOD的度数．

    （3）小明发现OE平分∠BOC，请你通过计算说明道理．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上点A表示的数为﹣7，点B表示的数为5，点C到点A，点B的距离相等，动点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动的时间为t（t＞0）秒．

    （1）点C表示的数是　 　；

    （2）求当t等于多少秒时，点P到达点B处；

    （3）点P表示的数是　 　（用含有t的代数式表示）；

    （4）求当t等于多少秒时，PC之间的距离为2个单位长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在平面直角坐标系中，点A的坐标为（0，a）,点B，点C的坐标分别为（-b，0），（b，0）.

    （1）如图，求点A，B，C的坐标；

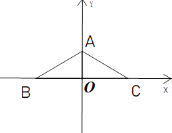
    （2）如图，若点D在第一象限且满足AD=AC，∠DAC=90°，求BD；

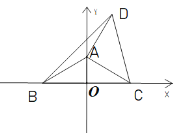
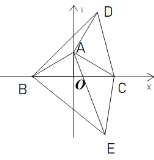
    （3）如图，在（2）的条件下，若在第四象限有一点E，满足∠BEC=∠BDC，请探究BE，CE，AE之间的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m，宽为n）的盒子底部（如图②），盒子底部未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分周长和是_________（用代数式表示）

    查看答案和解析>>

    同步练习册答案