
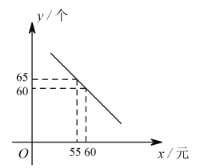
����Ŀ��ij������Ʒ�̵�����һ��ɱ�Ϊ 50 Ԫ�����涨�����ڼ䵥�۲����ڳɱ��ۣ��һ������ø��� 40%�����������֣������� ![]() �����������۵���
�����������۵��� ![]() ��Ԫ��֮��������ͼ��ʾ��һ�κ�����ϵ.
��Ԫ��֮��������ͼ��ʾ��һ�κ�����ϵ.
��1����ȷ��![]() ��
�� ![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2������������Ʒ�̵������������������õ�����Ϊ ![]() Ԫ����д������
Ԫ����д������ ![]() ��Ԫ�������۵���
��Ԫ�������۵��� ![]() ��Ԫ��֮��ĺ�����ϵʽ�����������۶�Ϊ����Ԫʱ�����̵�ɻ����������������Ƕ���Ԫ��
��Ԫ��֮��ĺ�����ϵʽ�����������۶�Ϊ����Ԫʱ�����̵�ɻ����������������Ƕ���Ԫ��
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
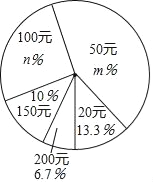
����Ŀ��ij��ѧ��һ�ΰ��ľ���У�ȫ��ͬѧ����ӻԾ���ֳ���˾��꼶��1����ȫ��ͬѧ�������������Ƴ����µ�ͳ�Ʊ���ͳ��ͼ��
��Ԫ�� | ��20 | ��50 | ��100 | 150 | 200 |
���������ˣ� | ��4 | ��12 | ��9 | 3 | 2 |
����m=_____��n=_____��
��������ѧ�������Ŀ����������λ����ƽ������
����������У��ѧ��2500�ˣ����Ƹ�Уѧ����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
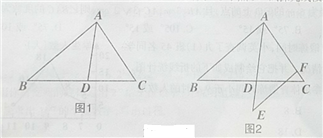
����Ŀ����֪����ͼ1��AD�ǡ�ABC�Ľ�ƽ���ߣ���AD=BD��
��1����֤����CDA�ס�CAB��
��2����AD=6��CD=5����AC��ֵ��
��3����ͼ2���ӳ�AD��E��ʹAE=AB����E����EF��AB����AC�ڵ�F����̽���߶�EF
���߶�AD�Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD��������A��AE��BC������ΪE������DE��FΪ�߶�DE��һ��������AFE=��B��
��1����֤����ADF�ס�DEC��
��2����AB=8��AD=![]() ��AF=
��AF=![]() ����AE�ij���
����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е������Ǽס��ҡ�������ÿ��ʮ�ε�����Եijɼ������Թ���Ϊ��������10����ÿ����λ1����1����
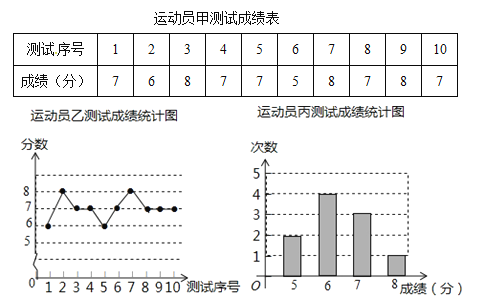
��1��д���˶�Ա�ײ��Գɼ�������Ϊ_________���˶�Ա�Ҳ��Գɼ�����λ��Ϊ_________���˶�Ա�����Գɼ���ƽ����Ϊ_________��
��2�����������˳ɼ��ķ���ֱ�ΪS��2=0.8��S��2=0.4��S��2=0.8�����ۺϷ�����������������ѡ��һλ����ɼ������ҽ�Ϊ�ȶ��Ľ���������Ϊ������������Ϊѡ˭�����ʣ�Ϊʲô��
��3���ס��ҡ��������֮����е�����ϰ��ÿ���˵��ȿ��ܵĴ������������������ȴӼ����д����������ֽ���ʱ��ص������еĸ����Ƕ��٣�������״ͼ���б��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
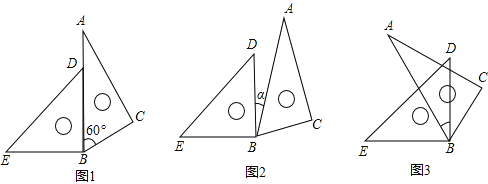
����Ŀ����1��ƽ���ڽ�һ�����ǰ尴��ͼ1��ʾ�ڷţ���EBC= �㣻
��2��ƽ���ڽ�һ�����ǰ尴��ͼ2��ʾ�ڷţ�����EBC=165������ô����= �㣻
��3��ƽ���ڽ�һ�����ǰ尴��ͼ3��ʾ�ڷţ���EBC=115�㣬�������Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����4��4�������������У���ABC�Ķ��㶼�ڸ���ϣ����н��۴�����ǣ�������
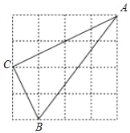
A. AB��5 B. ��C��90�� C. AC��2![]() D. ��A��30��
D. ��A��30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�![]() ��
��![]() ����D��x���ϣ������߶�
����D��x���ϣ������߶�![]() ���������˵�
���������˵�![]() ���ҵ�P��ʹ�õ�A��D��P���ɵ��������εĵ�Pǡ��ֻ��1��,����ѡ�����������������ĵ�D���겻������
���ҵ�P��ʹ�õ�A��D��P���ɵ��������εĵ�Pǡ��ֻ��1��,����ѡ�����������������ĵ�D���겻������![]() ����
����![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[����֪ʶ]�����dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������Ľ�ϣ��о��������Ƿ�����������Ҫ�Ĺ��ɣ�������A�㡢B���ʾ����Ϊa��b����A��B����֮��ľ���AB=|a��b|����a��b����ɼ�ΪAB=a��b���߶�AB���е�M��ʾ����Ϊ![]() ��
��
[�����龳]
��֪��������A��B���㣬�ֱ��ʾ����Ϊ��10��8����A��ÿ��3����λ���ٶ����������������˶�����B��ÿ��2����λ���������˶������˶�ʱ��Ϊt�루t��0����
![]()
[�ۺ�����]
��1���˶���ʼǰ��A��B����ľ���Ϊ ���߶�AB���е�M����ʾ���� ��
��2����A�˶�t�������λ�õĵ��ʾ����Ϊ ����B�˶�t�������λ�õĵ��ʾ����Ϊ �����ú�t�Ĵ���ʽ��ʾ��
��3�����ǰ�������ʽ�˶���A��B���㾭�������������������������ʾ������ʲô��
��4����A��B��������ʽ�����˶���ȥ���߶�AB���е�M�ܷ���ԭ���غϣ����ܣ�����˶�ʱ�䣬��ֱ��д���е�M���˶�������˶��ٶȣ������ܣ���˵�����ɣ�����A��B�����غϣ����е�MҲ��A��B�����غϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com