
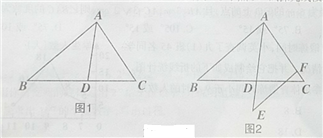
【题目】已知,如图1,AD是△ABC的角平分线,且AD=BD,
(1)求证:△CDA∽△CAB;
(2)若AD=6,CD=5,求AC的值;
(3)如图2,延长AD至E,使AE=AB,过E点作EF∥AB,交AC于点F,试探究线段EF
与线段AD的大小关系.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)根据角平分线的性质,得到∠BAD=∠CAD,再由等边对等角得到∠BAD=∠ABD,由等量代换得到∠CAD=∠B,即可得到结论;
(2)由相似三角形对应边成比例即可得到结论;
(3)结论为EF=AD.证明△BAD≌△EAF即可.
试题解析:(1)证明:∵AD是△ABC的角平分线,∴∠BAD=∠CAD.
∵AD=BD,∴∠BAD=∠ABD,∴∠CAD=∠B.∵∠C=∠C,∴△CDA∽△CAB.
(2)解:∵△CDA∽△CAB, ∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴AC=
,∴AC=![]() .
.
(3)答:EF= AD.理由如下:
∵EF∥AB,∴∠E=∠BAD.∵∠BAD=∠B,∴∠B=∠E.
∵AE=AB,∠BAD=∠EAF,∴△BAD≌△EAF,∴EF= AD.


科目:初中数学 来源: 题型:
【题目】如图,将边长为3的正三角形ABC放置在直线l上(AB与直线l重合),将正三角形ABC沿直线l向右做无滑动的滚动,正三角形ABC的任意一边与直线l重合时记录滚动次数,例如,正三角形ABC由图中位置①滚动到位置②时记录为滚动一次,当正三角形ABC由图中位置①开始滚动2018次时,点A经过的路径总长度为( )

A.2690πB.2692πC.4034πD.4036π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 ![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
,![]() ),如:数对(
),如:数对(![]() ,
,![]() ),(
),(![]() ,
,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(![]() ,
,![]() ),(
),(![]() ,
,![]() )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由.
(2)若(![]() ,
,![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
,![]() )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,3).
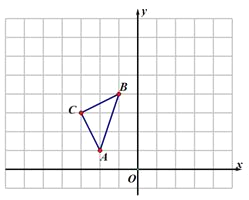
(1)画出△ABC绕点B逆时针旋转90°得到的△A1BC1.
(2)以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△ABC放大后的△A2B2C2,并写出A2点的坐标_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
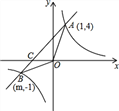
【题目】已知,如图,反比例函数y=![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式x+b>![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8.射线BD为∠ABC的平分线,交AC于点D.动点P以每秒2个单位长度的速度从点B向终点C运动.作PE⊥BC交射线BD于点E.以PE为边向右作正方形PEFG.正方形PEFG与△BDC重叠部分图形的面积为S.
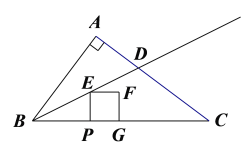
(1)求tan∠ABD的值.
(2)当点F落在AC边上时,求t的值.
(3)当正方形PEFG与△BDC重叠部分图形不是三角形时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:如果一个四位自然数,十位数字是千位数字的2倍与百位数字的差,个位数字是千位数字的2倍与百位数字的和,则我们称这个四位数“依赖数”,例如,自然数2135,其中3=2×2﹣1,5=2×2+1,所以2135是“依赖数”.
(1)请直接写出最小的四位依赖数;
(2)若四位依赖数的后三位表示的数减去百位数字的3倍得到的结果除以7余3,这样的数叫做“特色数”,求所有特色数.
(3)已知一个大于1的正整数m可以分解成m=pq+n4的形式(p≤q,n≤b,p,q,n均为正整数),在m的所有表示结果中,当nq﹣np取得最小时,称“m=pq+n4”是m的“最小分解”,此时规定:F(m)=![]() ,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=
,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=![]() =1,求所有“特色数”的F(m)的最大值.
=1,求所有“特色数”的F(m)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
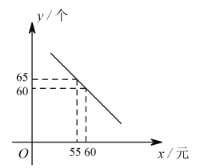
【题目】某体育用品商店试销一款成本为 50 元的排球,规定试销期间单价不低于成本价,且获利不得高于 40%。经试销发现,销售量 ![]() (个)与销售单价
(个)与销售单价 ![]() (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.
(1)试确定![]() 与
与 ![]() 之间的函数关系式;
之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获得的利润为 ![]() 元,试写出利润
元,试写出利润 ![]() (元)与销售单价
(元)与销售单价 ![]() (元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
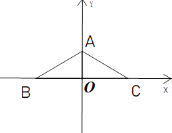
【题目】已知![]() ,在平面直角坐标系中,点A的坐标为(0,a),点B,点C的坐标分别为(-b,0),(b,0).
,在平面直角坐标系中,点A的坐标为(0,a),点B,点C的坐标分别为(-b,0),(b,0).
(1)如图,求点A,B,C的坐标;
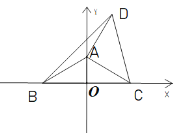
(2)如图,若点D在第一象限且满足AD=AC,∠DAC=90°,求BD;
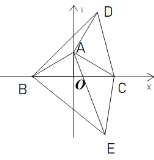
(3)如图,在(2)的条件下,若在第四象限有一点E,满足∠BEC=∠BDC,请探究BE,CE,AE之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com