
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8.射线BD为∠ABC的平分线,交AC于点D.动点P以每秒2个单位长度的速度从点B向终点C运动.作PE⊥BC交射线BD于点E.以PE为边向右作正方形PEFG.正方形PEFG与△BDC重叠部分图形的面积为S.
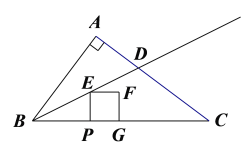
(1)求tan∠ABD的值.
(2)当点F落在AC边上时,求t的值.
(3)当正方形PEFG与△BDC重叠部分图形不是三角形时,求S与t之间的函数关系式.
【答案】(1)tan∠ABD=![]() ;(2)
;(2)![]() ;(3)①当
;(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.
【解析】
(1)过点D作DH⊥BC于点H,可得△ABD≌△HBD,所以CH=BC-AB=4.再由三角形相似即可求出DH=AD=3.根据三角函数定义即可解题.
(2)由(1)得BP=2PE,所以BP=2t,PE=PG=EF=FG=t,当点F落在AC边上时,FG=![]() CG,即可得到方程求出t.
CG,即可得到方程求出t.
(3)当正方形PEFG与△BDC重叠部分图形不是三角形时,分三种情况分别求出S与t之间的函数关系式,①当![]() 时,F点在三角形内部或边上,②当
时,F点在三角形内部或边上,②当![]() 时,如图:E点在三角形内部,F点在外部,此时重叠部分图形的面积S=S正方形-S△FMN,③当
时,如图:E点在三角形内部,F点在外部,此时重叠部分图形的面积S=S正方形-S△FMN,③当![]() 时,重叠部分面积为梯形MPGN面积,
时,重叠部分面积为梯形MPGN面积,
解:(1)如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8
根据勾股定理得BC=10
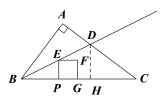
过点D作DH⊥BC于点H
∵△ABD≌△HBD,
∴BH=AH=6,DH=AD,
∴CH=4,
∵△ABC∽△HDC,
∴![]() ,
,
∴![]() ,
,
∴DH=AD=3,
∴tan∠ABD=![]() =
=![]() ,
,
(2)由(1)可知BP=2PE,依题意得:BP=2t,PE=PG=EF=FG=t,CG=10-3t,

当点F落在AC边上时,FG=![]() CG,
CG,
即![]() ,
,
![]() ,
,
(3)①当![]() 时,F点在三角形内部或边上,正方形PEFG在△BDC内部,
时,F点在三角形内部或边上,正方形PEFG在△BDC内部,
此时重叠部分图形的面积为正方形面积:![]() ,
,
②当![]() 时,如图:E点在三角形内部,F点在外部,
时,如图:E点在三角形内部,F点在外部,
∵GC=10-3t,NG=![]() CG=
CG=![]() (10-3t),FN=t-
(10-3t),FN=t-![]() (10-3t),FM=
(10-3t),FM=![]() ,
,

此时重叠部分图形的面积S=S正方形-S△FMN
![]() ,
,
③当![]() 时,重叠部分面积为梯形MPGN面积,如图:
时,重叠部分面积为梯形MPGN面积,如图:
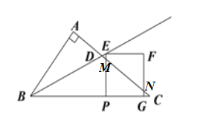
∵GC=10-3t,NG=![]() CG=
CG=![]() (10-3t),PC=10-2t,PM=
(10-3t),PC=10-2t,PM=![]() ,
,
∴![]() ,
,
综上所述:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
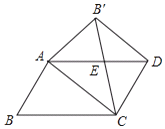
(发现与证明)ABCD中,AB≠BC,将△ABC沿AC翻折至△AB`C,连结B`D.
结论1:△AB`C与ABCD重叠部分的图形是等腰三角形;结论2:B`D∥AC;
(1)请证明结论1和结论2;
(应用与探究)
(2)在ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB`C,连接B`D![]() 若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形)
若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形)
查看答案和解析>>
科目:初中数学 来源: 题型:
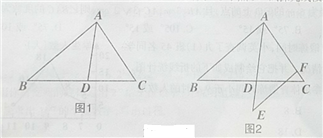
【题目】已知,如图1,AD是△ABC的角平分线,且AD=BD,
(1)求证:△CDA∽△CAB;
(2)若AD=6,CD=5,求AC的值;
(3)如图2,延长AD至E,使AE=AB,过E点作EF∥AB,交AC于点F,试探究线段EF
与线段AD的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
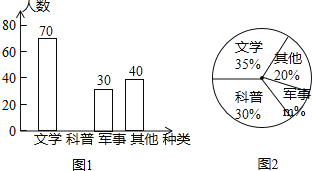
【题目】某学校在开展“书香校园”活动期间,对学生课外阅读的喜好进行抽样调查(每人只选一种书籍),将调查结果绘制成如图所示的两幅不完整的统计图,根据图中的信息,解答下列问题:
(1)这次调查的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;
(3)如果这所学校要添置学生课外阅读的书籍1500册,请你估计“科普”类书籍应添置多少册比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
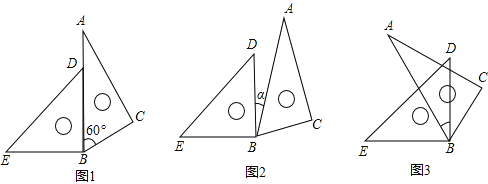
【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 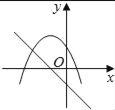 B.
B. 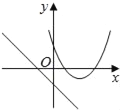 C.
C. 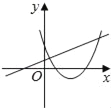 D.
D. 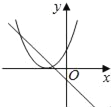
【答案】D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
【题型】单选题
【结束】
10
【题目】如图,已知菱形ABCD的周长为16,面积为![]() ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
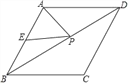
A. 2 B. 2![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com