
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
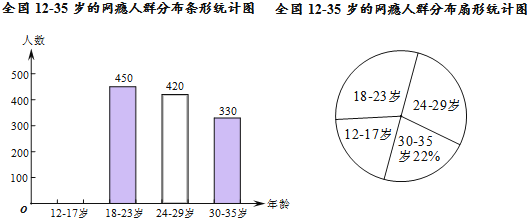
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人,并请补全条形统计图;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是 度;
(3)据报道,目前我国12﹣35岁“网瘾人数”约为2000万,请估计其中12﹣17岁的人数.
【答案】(1)1500,见解析;(2)108°;(3)400万人
【解析】
(1)根据30﹣35岁的人数除以所占的百分比,可得调查的人数,由各年龄段的人数之和等于总人数求得12﹣17岁人数可补全条形图;
(2)根据18﹣23岁的人数除以抽查的人数乘以360°,可得答案;
(3)根据总人数乘以12﹣17岁的人数所占的百分比,可得答案.
解:(1)这次抽样调查中调查的总人数为330÷22%=1500,
则12~17岁的人数为1500﹣(450+420+330)=300(人),
补全条形图如下:
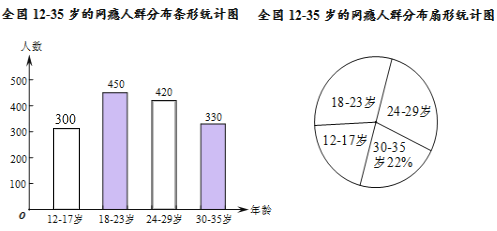
(2)扇形统计图中18﹣23岁部分的圆心角的度数是360°×![]() =108°,
=108°,
故答案为:108;
(3)2000×![]() =400(万人),
=400(万人),
答:估计其中12﹣17岁的人数为400万人.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】“你记得父母的生日吗?”这是我校九年级开展“感恩”主题活动设置的问题,有以下四个选项:A.父母生日都记得;B.只记得母亲生日;C.只记得父亲生日;D.父母生日都不记得.在随机调查了(1)班、(2)班各50名学生后,绘制出如图所示的统计图.
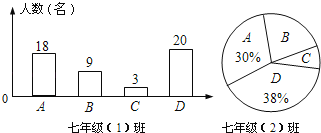
(1)据此推算,若九年级共1000名学生,其中“父母生日都不记得”的学生有多少名?
(2)若两个班中“只记得母亲生日”的学生占22%,则(2)班“只记得母亲生日”的学生所占百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
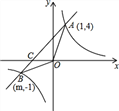
【题目】已知,如图,反比例函数y=![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式x+b>![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
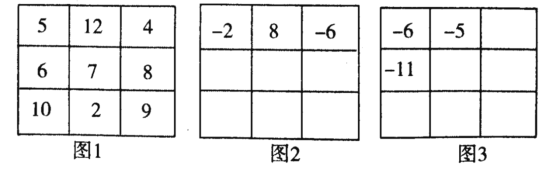
【题目】将九个数填在3×3(3行3列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,这样的图称为“广义的三阶幻方”,如图1就是一个满足条件的广义三阶幻方.图2、图3的广义三阶幻方中分别给出了三个数.请直接将图2、图3的其余6个数全填上;
(提示:三阶幻方的幻和=中心数字×3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:如果一个四位自然数,十位数字是千位数字的2倍与百位数字的差,个位数字是千位数字的2倍与百位数字的和,则我们称这个四位数“依赖数”,例如,自然数2135,其中3=2×2﹣1,5=2×2+1,所以2135是“依赖数”.
(1)请直接写出最小的四位依赖数;
(2)若四位依赖数的后三位表示的数减去百位数字的3倍得到的结果除以7余3,这样的数叫做“特色数”,求所有特色数.
(3)已知一个大于1的正整数m可以分解成m=pq+n4的形式(p≤q,n≤b,p,q,n均为正整数),在m的所有表示结果中,当nq﹣np取得最小时,称“m=pq+n4”是m的“最小分解”,此时规定:F(m)=![]() ,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=
,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=![]() =1,求所有“特色数”的F(m)的最大值.
=1,求所有“特色数”的F(m)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
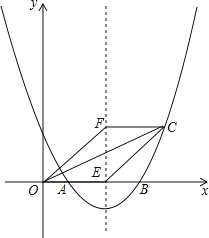
【题目】如图,抛物线![]() 与x轴交于点A(1,0)和B(4,0).
与x轴交于点A(1,0)和B(4,0).
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com