
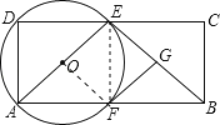
【题目】如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.
(1)若E是CD的中点时,证明:FG是⊙O的切线
(2)试探究:BE能否与⊙O相切?若能,求出此时DE的长;若不能,请说明理由.

【答案】(1)见解析;(2)点E不存在,BE不能与⊙O相切,理由见解析
【解析】
(1)要证明FG是⊙O的切线只要证明OF⊥FG即可;
(2)先假设BE能与⊙O相切,则AE⊥BE,即∠AEB=90°.设DE的长为x,然后用x表示出CE的长,根据勾股定理可得出一个关于x的一元二次方程,若BE能与⊙O相切,那么方程的解即为DE的长;若方程无解,则说明BE不可能与⊙O相切.
(1)连接OF、EF;
∵AE是⊙O的直径,AF⊥EF,
∵四边形ABCD是矩形,
∴∠DAB=∠D=90°,AB=CD,
∴四边形ADEF是矩形,
∴AF=DE,
∴EC=BF,
∵E是CD的中点,
∴F是AB的中点,
∴OF∥BE,
∵FG⊥BE,
∴OF⊥FG,
∴FG为⊙O的切线.
(2)若BE能与⊙O相切,因AE是⊙O的直径,则AE⊥BE,∠AEB=90°.
设DE=x,则EC=5﹣x.
由勾股定理得:AE2+EB2=AB2,
即(9+x2)+[(5﹣x)2+9]=25,
整理得x2﹣5x+9=0,
∵b2﹣4ac=25﹣36=﹣11<0,
∴该方程无实数根,
∴点E不存在,BE不能与⊙O相切.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
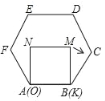
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是( )
A. 0.5B. 0.7C. ![]() ﹣1D.
﹣1D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 先化简,再求值:
(1)[x2+y2﹣(x+y)2+2x(x﹣y)]÷4x,其中x﹣2y=2
(2)(mn+2)(mn﹣2)﹣(mn﹣1)2,其中m=2,n=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
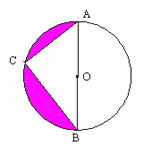
【题目】如图,⊙![]() 的半径为5,AB为直径,C是圆周上一点。
的半径为5,AB为直径,C是圆周上一点。
(1)求∠ACB的度数。
(2)若AC=AO,求阴影部分的面积(用含![]() 的代数式表示).
的代数式表示).
(3)当C点在圆周上移动时,AC、BC、AB三条线段的长度之间存在着恒定不变的关系,请你写出一种这样的关系,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
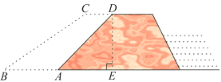
【题目】为做好汉江防汛工作,防汛指挥部决定对一段长为2500m重点堤段利用沙石和土进行加固加宽.专家提供的方案是:使背水坡的坡度由原来的1:1变为1:1.5,如图,若CD∥BA,CD=4米,铅直高DE=8米.
(1)求加固加宽这一重点堤段需沙石和土方数是多少?
(2)某运输队承包这项沙石和土的运送工程,根据施工方计划在一定时间内完成,按计划工作5天后,增加了设备,工效提高到原来的1.5倍,结果提前了5天完成任务,问按原计划每天需运送沙石和土多少m3?
查看答案和解析>>
科目:初中数学 来源: 题型:
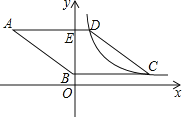
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
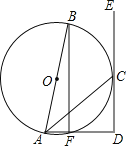
【题目】如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O于点F,∠AC平分∠BAD,连接BF.
(1)求证:AD⊥ED;
(2)若CD=4,AF=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com