
【题目】如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4
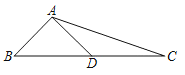
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)延长AD到点E,使ED=AD,然后连接CE即可;
(2)作AH⊥BD于H,如图,证明△ADB≌△EDC得到CE=AB=6,∠E=∠BAD,再利用勾股定理的逆定理得到△AEC为直角三角形,∠E=90°,则∠BAD=90°,然后利用面积法求AH即可.
解:(1)如图,△ECD为所作;
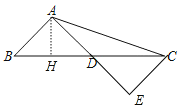
(2)作AH⊥BD于H,如图,
∵AD为中线,
∴BD=CD,
而AD=ED,∠ADB=∠EDC,
∴△ADB≌△EDC(SAS),
∴CE=AB=6,∠E=∠BAD,
在△AEC中,∵CE=6,AE=8,AC=10,
∴CE2+AE2=AC2,
∴△AEC为直角三角形,∠E=90°,
∴∠BAD=90°,
在Rt△BAD中,BD=![]() =2
=2![]() ,
,
∵![]() ×BD×AH=
×BD×AH=![]() ×AB×AD,
×AB×AD,
∴AH=![]() =
=![]() ,
,
即点A到BC的距离为![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P,已知BC=6,AH=4.当矩形DEFG面积最大时,HP的长是( )
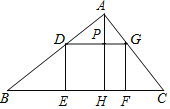
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
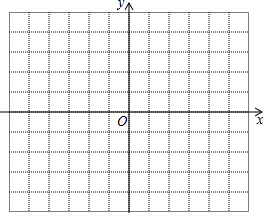
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于以AB为直径的⊙O,过点A作⊙O的切线,与BC的延长线相交于点D,在CB上截取CE=CD,连接AE并延长,交⊙O于点F,连接CF.
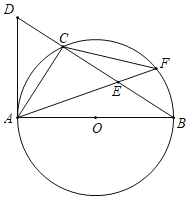
(1)求证:AC=CF;
(2)若AB=4,sinB![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、P、D、C都在在⊙O上,且四边形BCEP是平行四边形.
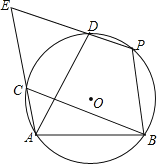
(1)证明:![]() =
=![]() ;
;
(2)若AE=BC,AB=![]() ,
,![]() 的长度是
的长度是![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两位同学在足球场上游戏,两人的运动路线如图1所示,其中AC=DB,小王从点A出发沿线段AB运动到点B,小林从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示,结合图象分析,下列说法正确的是( )
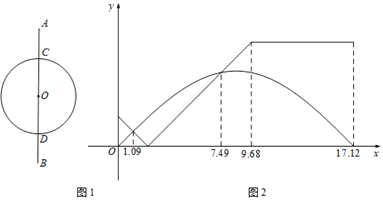
A. 小王的运动路程比小林的长
B. 两人分别在![]() 秒和
秒和![]() 秒的时刻相遇
秒的时刻相遇
C. 当小王运动到点D的时候,小林已经过了点D
D. 在![]() 秒时,两人的距离正好等于
秒时,两人的距离正好等于![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宣和中学图书馆今日购进甲、乙两种图书,每本甲种图书的进价比每本乙种图书的进价高20元,花780元购进甲种图书的数量与花540元购进乙种图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元;
(2)宣和中学购进甲、乙两种图书共70本,总购书费用不超过3950元,则最多购进甲种图书多少本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com