
【题目】根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
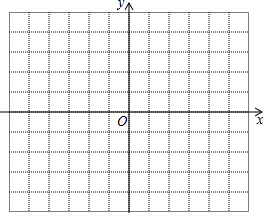
【答案】(1)﹣2,﹣1;(2)详见解析;(3)函数关于x=1对称;(4)0<m<2.
【解析】
(1)将点(0,0)、(1,3)代入函数y=x2+ax﹣4|x+b|+4,得到关于a、b的一元二次方程,解方程组即可求得;
(2)描点法画图即可;
(3)根据图象即可得到函数关于x=1对称;
(4)结合图象找,当x=﹣1时,y=﹣1;当x=1,y=3;则当0<m<2时,方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解.
解:(1)将点(0,0)、(1,3)代入函数y=x2+ax﹣4|x+b|+4(b<0),得 ,
,
解得a=﹣2,b=﹣1,
故答案为﹣2,﹣1;
(2)画出函数图象如图:
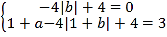
(3)该函数的一条性质:函数关于x=1对称;
(4)∵方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解
∴二次函数y=x2+ax﹣4|x+b|+4的图像与一次函数y=x+m至少有三个交点,
根据一次函数图像的变化趋势,
∴当0<m<2时,方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,
故答案为0<m<2.


科目:初中数学 来源: 题型:
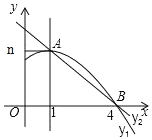
【题目】如图,是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,n),与x轴的一个交点B(4,0),直线y2=mx+d(m≠0)与抛物线交于A,B两点,下列结论:
①3a+b=0,②方程ax2+bx+c+1=n有两个相等的实数根,③b2=4a(c﹣n),④当1<x<4时,有y2>y1,⑤ax2+bx≤a+b,其中正确的结论是____(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,等边![]()
![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,点
,点![]() ,点
,点![]() 在第一象限.
在第一象限.
(1)若抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() ,求抛物线
,求抛物线![]() 的表达式.
的表达式.
(2)点![]() 是平面内一点,以点
是平面内一点,以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,现将抛物线
为顶点的四边形是平行四边形,现将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ,若抛物线
,若抛物线![]() 经过
经过![]() 、
、![]() 两点,求抛物线
两点,求抛物线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红灯笼,象征着阖家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对:物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.
①求出y与x之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
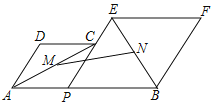
【题目】如图,已知AB=12,G、H是线段AB的三等分点,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,![]() =
=![]() ,M,N分别是对角线AC,BE的中点,在点P从点G运动到点H的过程中,MN的长度的取值范围是()
,M,N分别是对角线AC,BE的中点,在点P从点G运动到点H的过程中,MN的长度的取值范围是()
A.![]() ≤MN≤6B.
≤MN≤6B.![]() ≤MN≤
≤MN≤![]()
C.![]() ≤MN≤6D.
≤MN≤6D.![]() ≤MN≤
≤MN≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4
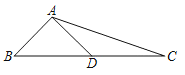
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=![]() ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com