
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 分类讨论 | B. | 数形结合 | C. | 公理化 | D. | 转化 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| +3 | -2 | 0 | +2 | -1 | -1 | +1 | +2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
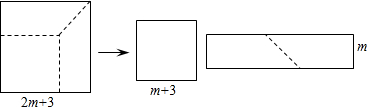
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50(1+x)2=146 | B. | 50+50(1+x)+50(1+x)2=146 | ||
| C. | 50(1+x)+50(1+x)2=146 | D. | 50+50(1+x)+50(1+2x)=146 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系:
某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com