
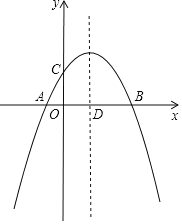
【题目】如图,抛物线y=ax2+![]() x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2(2)(
x+2(2)(![]() ,4)或(
,4)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )(3)(2,1)
)(3)(2,1)
【解析】
(1)利用待定系数法转化为解方程组即可.
(2)如图1中,分两种情形讨论①当CP=CD时,②当DP=DC时,分别求出点P坐标即可.
(3)如图2中,作CM⊥EF于M,设![]() 则
则![]() (0≤a≤4),根据S四边形CDBF=S△BCD+S△CEF+S△BEF
(0≤a≤4),根据S四边形CDBF=S△BCD+S△CEF+S△BEF![]() 构建二次函数,利用二次函数的性质即可解决问题.
构建二次函数,利用二次函数的性质即可解决问题.
解:(1)由题意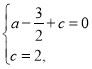
解得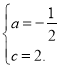
∴二次函数的解析式为![]()
(2)存在.如图1中,
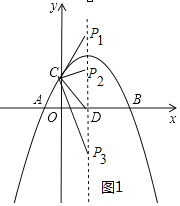
∵C(0,2),![]()
∴CD=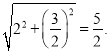
当CP=CD时,![]()
当DP=DC时, ![]()
综上所述,满足条件的点P坐标为![]() 或
或![]() 或
或![]()
(3)如图2中,作CM⊥EF于M,
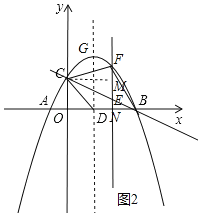
∵B(4,0),C(0,2),
∴直线BC的解析式为![]() 设
设![]()
∴![]() (0≤a≤4),
(0≤a≤4),
∵S四边形CDBF=S△BCD+S△CEF+S△BEF![]()
![]() ,
,
![]()
![]()
∴a=2时,四边形CDBF的面积最大,最大值为![]() ,
,
∴E(2,1).


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲同学手中藏有三张分别标有数字 的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为
的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为![]() .
.
【1】请你用树形图或列表法列出所有可能的结果.
【2】现制定这样一个游戏规则:若所选出的![]() 能使得
能使得![]() 有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释
有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).
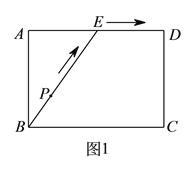

A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
若![]() ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)点(﹣5,﹣2)的“可控变点”坐标为 ;
(2)若点P在函数![]() 的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;
的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;
(3)若点P在函数![]() (
(![]() )的图象上,其“可控变点”Q的纵坐标y′ 的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′ 的取值范围是![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
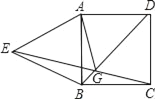
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
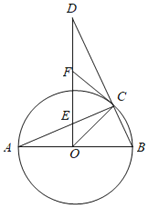
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com