
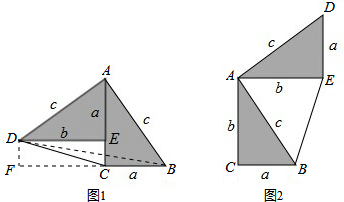
分析 连接BD,多边形ACBED的面积=△ABC的面积+△ABE的面积+△ADE的面积=$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab,多边形ACBED的面积=△ABC的面积+△ABD的面积+△BDE的面积=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),得出$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),即可得出结论.
解答 解:连接BD,如图所示: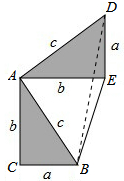
∵多边形ACBED的面积=△ABC的面积+△ABE的面积+△ADE的面积=$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab,
又∵多边形ACBED的面积=△ABC的面积+△ABD的面积+△BDE的面积=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),
∴$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),
整理得:a2+b2=c2.
故答案为:BD,$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab,$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a).
点评 本题考查了勾股定理的证明、三角形面积的计算方法、多边形面积的计算方法;熟练掌握勾股定理的证明方法,运用面积法证明勾股定理是常用的方法.


科目:初中数学 来源: 题型:解答题
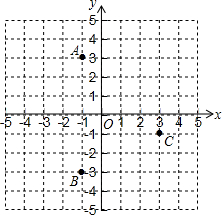 如图,分别求一个或一组平移,使得:
如图,分别求一个或一组平移,使得:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
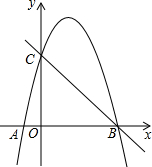 如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
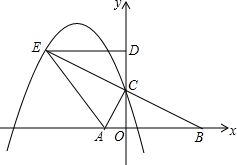 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.
如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com