
 如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A处测得建筑物CD的顶点C的俯角∠EAC=30°,测得底部D点的俯角∠EAD=45°.
如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A处测得建筑物CD的顶点C的俯角∠EAC=30°,测得底部D点的俯角∠EAD=45°.分析 (1)根据题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,利用BD=AB=60,求得两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=60,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.
解答 解:(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60米,
答:两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,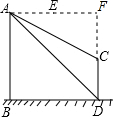
∴AF=BD=DF=60米,
在Rt△AFC中,∠FAC=30°,
∴CF=AF•tan∠FAC=60×$\frac{\sqrt{3}}{3}$=20$\sqrt{3}$米,
又∵FD=60米,
∴CD=60-20$\sqrt{3}$(米).
答:建筑物CD的高度为(60-20$\sqrt{3}$)米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正确标注仰角和俯角、熟记锐角三角函数的定义是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| 记数的次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
| 每小时进入旅游区的人数 | 318 | 310 | 310 | 286 | 280 | 312 | 284 |
| A. | 900000元 | B. | 1260000元 | C. | 191600元 | D. | 162000元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
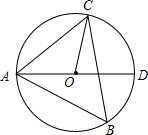 如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.
如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com