
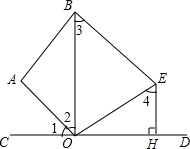
 如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.
如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.  举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:填空题
 如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.
如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子底端A′到墙根O的距离等于3m,同时梯子的顶端B下降到B′,那么BB′=7-2$\sqrt{11}$m.
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子底端A′到墙根O的距离等于3m,同时梯子的顶端B下降到B′,那么BB′=7-2$\sqrt{11}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB,直线y=mx-m恒过定点,且与AB有交点,求m的取值范围$\frac{3}{5}$≤m≤3.
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB,直线y=mx-m恒过定点,且与AB有交点,求m的取值范围$\frac{3}{5}$≤m≤3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,过⊙O上一点C作弦BA的垂线,交BA延长线于D点,连OA、CA,若AC平分∠OAD.
如图,过⊙O上一点C作弦BA的垂线,交BA延长线于D点,连OA、CA,若AC平分∠OAD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com