
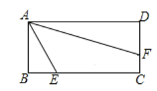
【题目】如图,在矩形ABCD中,AB=3,BC=6,点E,F分别在BC,CD上,若BE=![]() ,∠EAF=45°,则AF=_____.
,∠EAF=45°,则AF=_____.
【答案】![]()
【解析】
如图,作正方形ABNM,MN与AF交于点G,连接EG,延长EB至H,使BH=MG,连接AH,证△AMG≌△ABH,△GAE≌△HAE,根据全等三角形的性质得出EG=HE=BE+MG,设MG=x,根据全等三角形的性质得到用x表示出MG,根据勾股定理求出MG,根据相似三角形的性质求出DF,利用勾股定理即可求出AF的长.
如图,作正方形ABNM,MN与AF交于点G,连接EG,延长EB至H,使BH=MG,连接AH,

∵在正方形ABNM中,
∴∠AMG=∠ABH,AM=AB,
在△AMG和△ABH中,
∵ ,
,
∴△AMG≌△ABH(SAS),
∴∠BAH=∠GAM,AG=AH,
∴∠GAH=90°,
∴∠EAG=∠EAH=45°,
在△GAE和△HAE中,
∵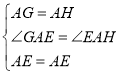 ,
,
∴△GAE≌△HAE(SAS),
∴EG=HE=BE+HB,
∴EG=BE+MG,
设MG=x,则NG=3-x,EG=x+![]() ,
,
在Rt△GEN中,EG2=NG2+NE2,即(x+![]() )2=(3﹣x)2+
)2=(3﹣x)2+![]() ,
,
解得:x=1,即MG=1,
∵MN∥CD,
∴△AGM∽△AFD,
∴![]() ,即
,即![]() ,
,
解得:DF=2,
∴![]()


科目:初中数学 来源: 题型:
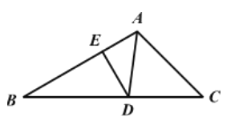
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题
(1)此次共调查了 名学生;
(2)将条形统计图1补充完整;
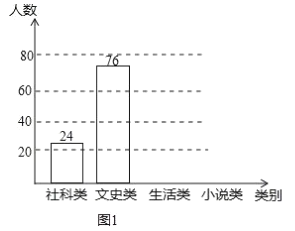
(3)图2中“社科类”所在扇形的圆心角为 度;
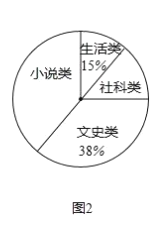
(4)若该校共有学生![]() 人,估计该校喜欢“社科类”书籍的学生人数.
人,估计该校喜欢“社科类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,手机已经成了我们生活中密不可分的一部分,为了解中学生在平时使用手机的情况(选项:A.和同学亲友聊天;B.学习查找资料;C.游戏娱乐;D.其他),某中学在全校范围内随机抽取了若干名学生进行调查,要求每名学生必须且只能选择其中一项,并将调查结果绘制成如下两幅不完整的统计图.
根据以上信息解答下列问题:
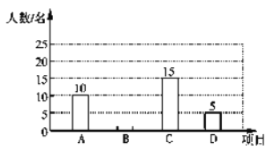
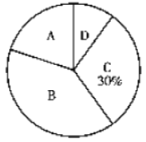
(1)本次抽样调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若该中学共有![]() 名学生,请你估计该中学利用手机学习查找资料的学生有多少名.
名学生,请你估计该中学利用手机学习查找资料的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )
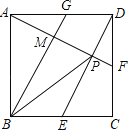
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸想给妈妈送张美容卡作为生日礼物,小明家附近有 3 家美容店,爸爸不知 如何选择,于是让小明对 3 家店铺顾客的满意度做了调查:
|
|
| 合计 | |
美容店 A | 53 | 28 | 19 | 100 |
美容店 B | 50 | 40 | 10 | 100 |
美容店 C | 65 | 26 | 9 | 100 |
(说明:顾客对于店铺的满意度从高到低,依次为 3 个笑脸,2 个笑脸,1 个笑脸) 小明选择将_____(填“A”、“ B”或“C”)美容店推荐给爸爸,能使妈妈获得满意体验可能性最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com