
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 
【答案】![]() 或3
或3
【解析】解:当△CEB′为直角三角形时,有两种情况: 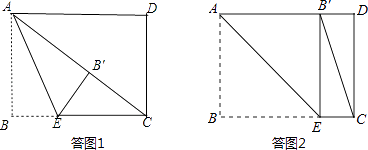
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC= ![]() =5,
=5,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5﹣3=2,
设BE=x,则EB′=x,CE=4﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2 ,
∴x2+22=(4﹣x)2 , 解得x= ![]() ,
,
∴BE= ![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,∴BE=AB=3.
综上所述,BE的长为 ![]() 或3.
或3.
故答案为: ![]() 或3.
或3.
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( ) 
A.1:3
B.1:5
C.1:6
D.1:11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线
绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线![]() 于点MN,
于点MN,![]() 于点H.
于点H.
![]() 如图
如图![]() ,当
,当![]() 点A旋转到
点A旋转到![]() 时,请你直接写出AH与AB的数量关系;
时,请你直接写出AH与AB的数量关系;
![]() 如图
如图![]() ,当
,当![]() 绕点A旋转到
绕点A旋转到![]() 时,
时,![]() 中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.
中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:
(1)“基础电价”是____________元 ![]() 度;
度;
(2)求出当x>240 时,y与x的函数表达式;
(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.

(1)当AB=2时,求GC的长;
(2)求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点![]() 点P第1次向上跳动1个单位至点
点P第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位至点
,第3次向上跳动1个单位至点![]() ,第4次向右跳动3个单位至点
,第4次向右跳动3个单位至点![]() ,第5次又向上跳动1个单位至点
,第5次又向上跳动1个单位至点![]() ,第6次向左跳动4个单位至点
,第6次向左跳动4个单位至点![]() ,
,![]() 照此规律,点P第100次跳动至点
照此规律,点P第100次跳动至点![]() 的坐标是
的坐标是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y= ![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
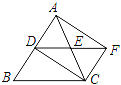
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在计算一个多边形(每个内角小于180°)的内角和时,由于粗心少算了一个内角,
结果得到的总和是2018°,则少算了这个内角的度数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com