
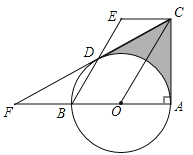
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=6,求图中阴影部分的面积(结果保留根号和π)
【答案】(1)证明见解析;(2)9![]() ﹣3π
﹣3π
【解析】试题分析:(1)、连接OD,根据平行四边形的性质得出∠AOC=∠OBE,∠COD=∠ODB,结合OB=OD得出∠DOC=∠AOC,从而证明出△COD和△COA全等,从而的得出答案;(2)、首先根据题意得出△OBD为等边三角形,根据等边三角形的性质得出EC=ED=BO=DB,根据Rt△AOC的勾股定理得出AC的长度,然后根据阴影部分的面积等于两个△AOC的面积减去扇形OAD的面积得出答案.
试题解析:(1)如图连接OD.
∵四边形OBEC是平行四边形,∴OC∥BE,∴∠AOC=∠OBE,∠COD=∠ODB,
∵OB=OD,∴∠OBD=∠ODB,∴∠DOC=∠AOC,
在△COD和△COA中, ,∴△COD≌△COA,∴∠CDO=∠CAO=90°,
,∴△COD≌△COA,∴∠CDO=∠CAO=90°,
∴CF⊥OD, ∴CF是⊙O的切线.
(2)∵∠F=30°,∠ODF=90°,∴∠DOF=∠AOC=∠COD=60°,
∵OD=OB,∴△OBD是等边三角形,∴∠4=60°,∵∠4=∠F+∠1,∴∠1=∠2=30°,
∵EC∥OB,∴∠E=180°﹣∠4=120°,∴∠3=180°﹣∠E﹣∠2=30°,∴EC=ED=BO=DB,
∵EB=6,∴OB=OD═OA=3, 在Rt△AOC中,∵∠OAC=90°,OA=3,∠AOC=60°,
∴AC=OAtan60°=3![]() , ∴S阴=2S△AOC﹣S扇形OAD=2×
, ∴S阴=2S△AOC﹣S扇形OAD=2×![]() ×3×3
×3×3![]() ﹣
﹣![]() =9
=9![]() ﹣3π.
﹣3π.



 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)若原方程的一根大于3,另一根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
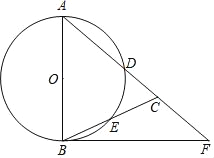
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交AC、BC于点D、E,点F在AC的延长线上,且∠A=2∠CBF.
(1)求证:BF与⊙O相切.
(2)若BC=CF=4,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,学校准备修建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形的高AM=3米,∠ABC=60°.设AE=x米(1≤x≤2),矩形EFGH的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,在四个三角形内种植绿色花草.已知:红色和绿色植物的价格为200元/米2,100元/米2,当x为何值时,购买花卉所需的总费用最低,并求出最低总费用(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有![]() 个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共
个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共![]() 组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做
组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做![]() 次试验,汇总起来后,摸到红球次数为
次试验,汇总起来后,摸到红球次数为![]() 次.
次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
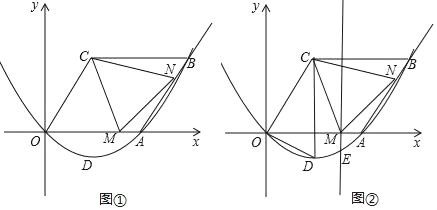
【题目】如图抛物线y=ax2+bx,过点A(4,0)和点B(6,2![]() ),四边形OCBA是平行四边形,点M(t,0)为x轴正半轴上的点,点N为射线AB上的点,且AN=OM,点D为抛物线的顶点.
),四边形OCBA是平行四边形,点M(t,0)为x轴正半轴上的点,点N为射线AB上的点,且AN=OM,点D为抛物线的顶点.
(1)求抛物线的解析式,并直接写出点D的坐标;
(2)当△AMN的周长最小时,求t的值;
(3)如图②,过点M作ME⊥x轴,交抛物线y=ax2+bx于点E,连接EM,AE,当△AME与△DOC相似时.请直接写出所有符合条件的点M坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】创意产品蕴含着很多商机,我市某文化创意公司,销售A,B两种创意产品,其中A产品的定价是每件20元,B产品的定价是每件30元.
(1)该公司按定价售出A,B两种产品共600件,若销售总额不低于15000元,则至少销售B产品多少件?
(2)2017年8月,该公司按定价售出A产品300件,B产品400件.2017年9月,公司根据市场情况,适当调整A,B产品的售价,A产品的售价比定价增加了a%,销量与8月保持不变;B产品的售价比定价减少了a%,销量比8月份增加了a%,结果9月份A,B产品的销售总额比8月份增加了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
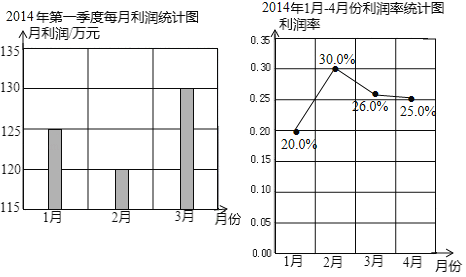
【题目】来自某综合市场财务部的报告表明,商场2014年1﹣4月份的投资总额一共是2065万元,商场2014年第一季度每月利润统计图和2014年1﹣4月份利润率统计图如下(利润率=利润÷投资金额).则商场2014年4月份利润是__万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com