
【题目】如图,已知![]() 两点的坐标分别为
两点的坐标分别为![]() 将线段
将线段![]() 向右平移
向右平移![]() 个单位到线段
个单位到线段![]() 连接
连接![]() 得四边形
得四边形![]() .
.
(1)则点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ,
的坐标为 ,![]() ;
;
(2)如图①,若点![]() 为四边形
为四边形![]() 内的一点,且
内的一点,且![]() 求
求![]() 的值.
的值.

(3)如图②,若点![]() 为四边形
为四边形![]() 内的一点(包括边界).且
内的一点(包括边界).且![]() 当
当![]() 面积取最大值时,求此时对应的点
面积取最大值时,求此时对应的点![]() 的坐标和最大面积的值.[提示:
的坐标和最大面积的值.[提示:![]() ]
]
科目:初中数学 来源: 题型:
【题目】如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值为( ) 
A.1
B.2
C.3
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和对“抢红包”所持态度情况进行了调查,并将调查结果绘成了条形统计图和扇形统计图.
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?
(3)请估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.

(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求:
,求:![]() 的值;
的值;
②已知:![]() ,
,![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,且
,且![]() .连接
.连接![]() 交对角线
交对角线![]() 于
于![]() ,连接
,连接![]() .下列结论:
.下列结论:

①![]() ;②
;②![]() 为等边三角形;
为等边三角形;
③![]() ; ④
; ④![]() .其中结论正确的是
.其中结论正确的是
A.只有①② | B.只有①②④ |
C.只有③④ | D.①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )
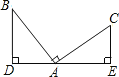
A. AD=AE B. AB=AC C. BD=AE D. AD=CE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com