
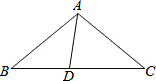
 如图,在△ABC中,∠B=24°,∠C=30°,D为BC边上一点,AB=CD,连接AD,求证:△DBA∽△ABC.
如图,在△ABC中,∠B=24°,∠C=30°,D为BC边上一点,AB=CD,连接AD,求证:△DBA∽△ABC. 分析 在△DBA与△ABC中,有一个公共角相等,所以欲证明△DBA∽△ABC,只需推知∠BAD=∠CAB,利用“两角法”证得两个三角形相似即可.
解答 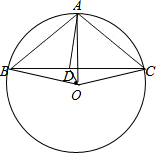 证明:如图,作△ABC的外接圆圆O,连接OB、OC、OA、OD.则OA=OB=OC,
证明:如图,作△ABC的外接圆圆O,连接OB、OC、OA、OD.则OA=OB=OC,
∵∠ACB=30°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=∠BAO=∠AOB=60°;
同理,∠BOC=2∠BAC=48°,
∵AB=CD,
∴OC=CD,
∴∠OCB=∠OBC=66°,
∴∠ACO=66°-30°=36°.
∵OA=OC,
∴∠COD=∠CDO=72°.
又∵∠AOC=180°-2×36°=108°,
∴∠AOD=108°-72°=36°.
∵∠OAD=36°,
∴AD=OD.
∵∠AOB°,
∴∠BOD=60°-36°=24°.
在△ABD与△OBD中,$\left\{\begin{array}{l}{AD=OD}\\{∠BAD=∠BOD}\\{AB=OB}\end{array}\right.$,
∴△ABD≌△OBD(SAS),
∴∠ABD=∠OBD=$\frac{1}{2}$∠ABO=30°.
∴∠BAD=∠CAB,
∴△DBA∽△ABC.
点评 本题考查了相似三角形的判定与性质和全等三角形的判定与性质.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
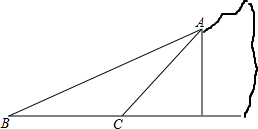 因山体滑坡,需将一段50米长的滑坡体清除,滑坡体横截面是如图所示的△ABC.测得堡坎坡面AC的坡度是1:1,滑坡体坡面AB的坡角是30°,滑坡体底宽BC=13米.
因山体滑坡,需将一段50米长的滑坡体清除,滑坡体横截面是如图所示的△ABC.测得堡坎坡面AC的坡度是1:1,滑坡体坡面AB的坡角是30°,滑坡体底宽BC=13米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com