
分析 根据实数与数轴上的点一一对应对①进行判断;根据垂线段最短对②进行判断;根据平行线的判定方法对③进行判断;根据无理数的定义对④进行判断;根据命题由题设与结论组成可对⑤进行判断;根据过直线外一点有且只有一条直线平行于已知直线对⑥进行判断.
解答 解:实数与数轴上的点一一对应,所以①正确;
垂线段最短,所以②正确;
若a⊥b,b⊥c,则a∥c,所以③正确;
无限不循环小数是无理数,所以④错误;
“同旁内角互补,两直线平行”的题设是“同旁内角互补”,结论是“两直线平行”,所以⑤正确;
过直线外一点有且只有一条直线平行于已知直线,所以⑥错误.
故答案为①②③⑤.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
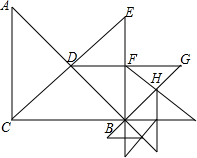 如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,CD⊥AB,垂足为D,以BD为一条直角边向三角形外作第二个等腰Rt△BDE,再以BF为一条直角边向三角形外作第三个等腰Rt△BFG,如此下去,如果Rt△ABC的斜边为记为c1,论上述方法所作的等腰直角三角形的斜边依次记为c2、c3、c4、…、cn,则c2015=$\frac{(\sqrt{2})^{2014}}{{2}^{2013}}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,CD⊥AB,垂足为D,以BD为一条直角边向三角形外作第二个等腰Rt△BDE,再以BF为一条直角边向三角形外作第三个等腰Rt△BFG,如此下去,如果Rt△ABC的斜边为记为c1,论上述方法所作的等腰直角三角形的斜边依次记为c2、c3、c4、…、cn,则c2015=$\frac{(\sqrt{2})^{2014}}{{2}^{2013}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
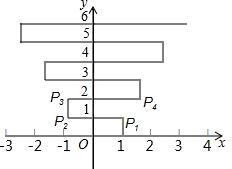 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )| A. | (100,50) | B. | (50,50) | C. | (25,50) | D. | (26,50) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
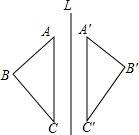 如图,△ABC与△A′B′C′关于直线L对称,若∠A=60°,∠C′=45°,则∠B的度数是( )
如图,△ABC与△A′B′C′关于直线L对称,若∠A=60°,∠C′=45°,则∠B的度数是( )| A. | 105° | B. | 75° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )| A. | $\frac{12}{7}$ | B. | 2 | C. | $\frac{12}{5}$或2 | D. | $\frac{12}{7}$或2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com