
【题目】如图,![]() 中,
中,![]() 和
和![]() 分别平分
分别平分![]() 和
和![]() 的外角
的外角![]() ,一动点
,一动点![]() 在
在![]() 上运动,过点
上运动,过点![]() 作
作![]() 的平行线与
的平行线与![]() 和
和![]() 的角平分线分别交于点
的角平分线分别交于点![]() 和点
和点![]() .
.

![]() 求证:当点
求证:当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 为矩形,说明理由;
为矩形,说明理由;
![]() 在第
在第![]() 题的基础上,当
题的基础上,当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 为正方形,说明理由.
为正方形,说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC 和△CDE 都是等腰直角三角形,∠ACB=∠ECD=90°,D 为 AB 边上一点.如下结论:

①△ACE≌△BCD; ②△ADE 是直角三角形; ③AD2+BD2=2CD2; ④AE=AC, 其中正确的结论有( )
A.①③④B.①②③C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
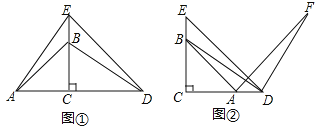
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级共有300位学生.为了解该年级学生地理、生物两门课程的学习情况,从中随机抽取60位学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理和分析,下面给出了部分信息.
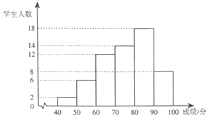
信息1:如图是地理课程成绩的条形统计图 (数据分成6组:第一组40≤![]() <50;第二组50≤
<50;第二组50≤![]() <60;第三组60≤
<60;第三组60≤![]() <70;第四组70≤
<70;第四组70≤![]() <80;第五组80≤
<80;第五组80≤![]() <90;第六组90≤
<90;第六组90≤![]() ≤100):
≤100):
信息2:地理课程测试在第四组70≤![]() <80的成绩是:
<80的成绩是:
70 71 71 71 73 73 75 75 76.5 76.5 78 78 79 79.5
信息3:地理、生物两门课程成绩的平均数、中位数、众数如下表:
课程 | 平均数 | 中位数 | 众数 |
地理 | 73.8 |
| 83.5 |
生物 | 72.2 | 70 | 82 |
根据以上信息,回答下列问题:
(1)所抽取的60位学生地理课程成绩的中位数落在第几组?写出这60位学生地理课程测试成绩的中位数![]() ;
;
(2)在此次测试中,某学生的地理课程成绩为75分,生物课程成绩为71分,该生成绩排名更靠前的课程是地理还是生物?说明理由;
(3)假设该年级学生都参加此次测试,估计地理课程成绩超过73.8分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△EDC.
(1)若DE∥BC(如图1),判断△ABC的形状并说明理由.
(2)连结BE,交AC于F,点H是CE上的点,且CH=CF,连结DH交BE于K(如图2).求证:∠DKF=∠ACB

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题解决:
问题解决:![]() 如图1,在平面直角坐标系xOy中,一次函数
如图1,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角
与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角![]() ,
,![]() ,点A、B的坐标分别为A______、B______.
,点A、B的坐标分别为A______、B______.
![]() 求
求![]() 中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点
中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点![]() 请你借助小明的思路,求出点C的坐标;
请你借助小明的思路,求出点C的坐标;
![]() 类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标
类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标![]() ,点B坐标
,点B坐标![]() ,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数
,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数![]() 图象上一动点,若
图象上一动点,若![]() 是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.
是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:

设某户每月用水量x(立方米),应交水费y(元)
(1)a= ,c=
(2)当x≤6,x≥6时,分别求出y于x的函数关系式
(3)若该户11月份用水量为8立方米,求该户11 月份水费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com