
【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.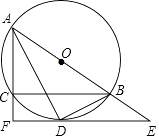
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.

(1)如图 1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式)
(3)比较图 1,图 2 的阴影部分面积,可以得到乘法公式 (用式子表达)
(4)应用所得的公式计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).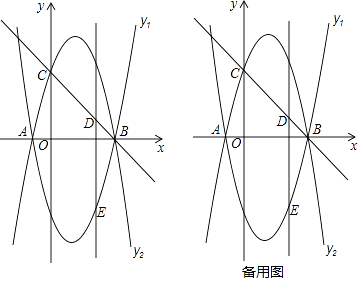
(1)求抛物线y1的函数解析式;
(2)如图①,将抛物线y1沿x轴翻折得到抛物线y2 , 抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表
身高分组 | 频数 | 频率 |
152≤ x<155 | 3 | 0.06 |
155≤ x<158 | 7 | 0.14 |
158≤ x<161 | m | 0.28 |
161≤ x<164 | 13 | n |
164≤ x<167 | 9 | 0.18 |
167≤ x<170 | 3 | 0.06 |
170≤ x<173 | 1 | 0.02 |

根据以上统计图表完成下列问题:
(1)统计表中m=____,n=____;并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( )
A.3
B.4
C.4.8
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中,且A![]() 、B
、B![]() 、C
、C![]() .将其平移后得到
.将其平移后得到![]() ,若A,B的对应点是
,若A,B的对应点是![]() ,
,![]() ,C的对应点
,C的对应点![]() 的坐标是
的坐标是![]() .
.
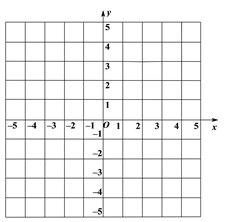
(1)在平面直角坐标系中画出△ABC;
(2)写出点![]() 的坐标是_____________,
的坐标是_____________,![]() 坐标是___________;
坐标是___________;
(3)此次平移也可看作![]() 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com