
【题目】乘法公式的探究及应用.

(1)如图 1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式)
(3)比较图 1,图 2 的阴影部分面积,可以得到乘法公式 (用式子表达)
(4)应用所得的公式计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() )
)
【答案】(1)a2-b2;(2)a-b,a+b,(a+b)(a-b);(3)(a+b)(a-b)=a2-b2;(4)![]() .
.
【解析】
(1)小题1:利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便计算.
(1)利用正方形的面积公式可知:阴影部分的面积=a2-b2;
故答案为:a2-b2;
(2)由图可知矩形的宽是a-b,长是a+b,所以面积是(a+b)(a-b);
故答案为:a-b,a+b,(a+b)(a-b);
(3)(a+b)(a-b)=a2-b2(等式两边交换位置也可);
故答案为:(a+b)(a-b)=a2-b2;
(4)(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() )
)
=(1-![]() )(1+
)(1+![]() )(1-
)(1-![]() )(1+
)(1+![]() )(1-
)(1-![]() )(1+
)(1+![]() )…(1-
)…(1-![]() )(1+
)(1+![]() )(1-
)(1-![]() )(1+
)(1+![]() )
)
=![]() ×
×![]()
=![]()
![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】根据实验结果表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度![]() 与所挂的物体的重量
与所挂的物体的重量![]() 间有下表的关系,下列说法不正确的是( )
间有下表的关系,下列说法不正确的是( )
| 0 | 1 | 2 | 3 | 4 |
| 20 | 21 | 22 | 23 | 24 |
A.![]() 与
与![]() 都是变量,且
都是变量,且![]() 是自变量,
是自变量,![]() 是因变量
是因变量
B.弹簧不挂重物时的长度为![]()
C.随着所挂物体重量的增加,弹簧长度逐渐变长
D.所挂物体的重量每增加![]() ,弹簧长度增加
,弹簧长度增加![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 的解是
的解是![]() ,求关于
,求关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 的解.
的解.
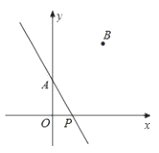
(2)如图,点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、![]() ,点
,点![]() 为
为![]() 轴上的一个动点,若点
轴上的一个动点,若点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 轴上,写出点
轴上,写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )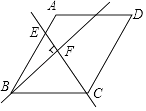
A.![]()
B.2 ![]()
C.![]() π
π
D.![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据图中信息解答下列问题:
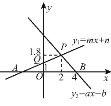
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.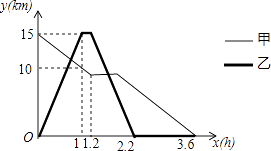
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com