Question

【题目】如图，AB是⊙O的直径，AC是弦，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E，连接BD．

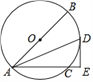
（1）求证：DE是⊙O的切线；

（2）若，AD=4，求CE的长．

Answer 1

【答案】（1）证明见解析;（2）CE=2．

【解析】试题分析: （1）连接OD，欲证明DE是⊙O的切线，只要证明OD⊥DE即可．

（2）利用相似三角形的判定和性质得出AB，利用勾股定理求出BD，进而解答即可．

试题解析:

（1）证明：连接OD．

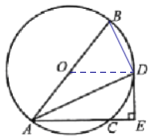
∵OA=OD，

∴∠BAD=∠ODA．

∵AD平分∠BAC，

∴∠BAD=∠DAC．

∴∠ODA=∠DAC．

∴OD∥AE．

∵DE⊥AE，

∴OD⊥DE．

∴DE是⊙O的切线；

（2）∵OB是直径，

∴∠ADB=90°．

∴∠ADB=∠E．

又∵∠BAD=∠DAC，

∴△ABD∽△ADE．

∴．

∴AB=10．

由勾股定理可知．

连接DC，

∴．

∵A，C，D，B四点共圆．

∴∠DCE=∠B．

∴△DCE∽△ABD．

∴．

∴CE=2．