练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

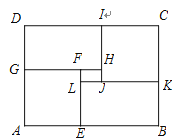
    【题目】在矩形ABCD中，AB=8，BC=6，将矩形按图示方式进行分割，其中正方形AEFG与正方形JKCI全等，矩形GHID与矩形EBKL全等．

    （1）当矩形LJHF的面积为时，求AG的长；

    （2）当AG为何值时，矩形LJHF的面积最大．

    【答案】（1）或；（2）.

    【解析】试题分析： 设AG=x，DG=6-x ，BE=8-x，FL=x-(6-x)=2x-6，LJ=8-2x，

    矩形 ，即可求出的长度.

    设矩形LJHF的面积为S，根据配方法求出面积的最大值.

    试题解析：（1）正方形AEFG和正方形JKCI全等，矩形GHID和矩形EBKL全等，

    设AG=x，DG=6-x ，BE=8-x，FL=x-(6-x)=2x-6，LJ=8-2x，

    方法1： 矩形 ，

    ∴，

    ∴， AG=或AG=．

    方法2： S矩形LIHF=S矩形ABCD-2S矩形DGHI-2S正方形AEFG.

    ，

    ∴， AG=或AG=．

    （2）设矩形LJHF的面积为S，

    ，

    .

    ,

    ，

    S有最大值，

    当AG= 时，矩形LJHF的面积最大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某公司有A、B两种型号的客车，它们的载客量、每天的租金如表所示：

    A型号客车

    B型号客车

    载客量(人/辆)

    45

    30

    租金(元/辆)

    600

    450

    已知某中学计划租用A、B两种型号的客车共10辆，同时送七年级师生到沙家参加社会实践活动，已知该中学租车的总费用不超过5600元．

    (1)求最多能租用多少辆A型号客车？

    (2)若七年级的师生共有380人，请写出所有可能的租车方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

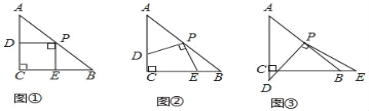
    【题目】如图，在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点．如图①、②、③是旋转三角板得到的图形中的3种情况，研究：

    （1）三角板绕点P旋转，观察线段PD与PE之间有什么数量关系？结合图②说明理由．

    （2）三角板绕点P旋转，△PCE是否能成为等腰三角形？若能，指出所有情况（直接写答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC中，∠ABC与∠ACB的平分线交于点P，根据下列条件，求∠BPC的度数．

    （1）若∠A=50°，则∠BPC=　　；

    （2）从上述计算中，我们能发现：∠BPC=　　（用∠A表示）；

    （3）如图2，若BP，CP分别是∠ABC与∠ACB的外角平分线，交于点P，则∠BPC=　　．（用∠A表示），并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有甲、乙两个不透明的布袋，甲袋中有3个完全相同的小球，分别标有数字0，1和2；乙袋中有3个完全相同的小球，分别标有数字1，2和3，小明从甲袋中随机取出1个小球，记录标有的数字为x，再从乙袋中随机取出1个小球，记录标有的数字为y，这样确定了点M的坐标(x，y)．

    （1）写出点M所有可能的坐标；

    （2）求点M在直线上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明、小红和小光共解出了100道数学题目，每人都解出了其中的60道题目，如果将其中只有1人解出的题目叫做难题，2人解出的题目叫做中档题，3人都解出的题目叫做容易题，那么难题比容易题多________道.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形 ABCD中，对角线 AC， BD交于点O，

    (1)若AO=BD，求证：四边形 ABCD为矩形；

    (2) 若 AE BD于点E，CF BD于点F，求证：AE CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长均为1个单位的正方形网格图中，建立了平面直角坐标系xOy，按要求解答下列问题：

    （1）写出△ABC三个顶点的坐标；

    （2）画出△ABC向右平移6个单位后得到的图形△A1B1C1；

    （3）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】田中数学兴趣小组发现，很多同学矿泉水没有喝完便扔掉，造成极大的浪费.为増强问学们的节水意识，小组成员在学校的春季运动会上，随机对部分同学半天时间内喝矿泉水的浪费情况进行了问卷调查(半天时间每人按一瓶500mL的矿泉水量计算，问卷中将间学们仍掉的矿泉水瓶中剩余水里大致分为四种:A：全部喝完；B.喝剩约满瓶的，C.喝剩约满瓶的；D.喝剩约满瓶的.小组成员将收集的调査问卷进行数据整理，并根据整理结果绘制了如图所示的两幅不完整的统计图，请根据统计图提供的信息，解答下列问题:

    （1）此次问卷共调查多少人；

    （2）请补全条形统计图；

    （3）计算平均每人半天浪费的矿泉水约为多少亳升；

    （4）请估计这次春季运动会全校名同学半天浪费的水量相当于多少瓶矿泉水(每瓶按计算).

    查看答案和解析>>

    同步练习册答案