
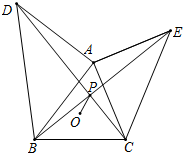
 如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是5-$\frac{5}{3}\sqrt{3}$.
如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是5-$\frac{5}{3}\sqrt{3}$. 分析 根据已知条件证明△DAC≌△BAE,得到∠DPB=90°,证明点P在以BC为直径的圆上,再在△BOC中,求出OH的长,得到答案.
解答 解:如图,∵∠BAD=∠CAE=90°,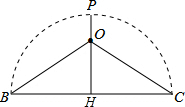
∴∠DAC=∠BAE,
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
∴∠PDB+∠PBD=90°,
∴∠DPB=90°,
∴点P在以BC为直径的圆上,
∵外心为O,∠BAC=60°,
∴∠BOC=120°,又BC=10,
∴OH=$\frac{5}{3}\sqrt{3}$,
所以OP的最小值是5-$\frac{5}{3}\sqrt{3}$.
点评 本题考查的是三角形的外接圆的知识,灵活运用等腰直角三角形的性质、直径所对的圆周角是直角和解直角三角形的知识是解题的关键,解答本题时,要确定OP在什么情况下最小.


科目:初中数学 来源: 题型:解答题
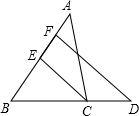 如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D三点在同一直线上,∠D=42°,当∠B的度数是多少时,EC∥FD?说明理由.
如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D三点在同一直线上,∠D=42°,当∠B的度数是多少时,EC∥FD?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | n(n-1) | B. | n(n+1) | C. | (n+1)(n-1) | D. | n2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
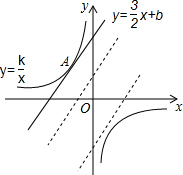 如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.
如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
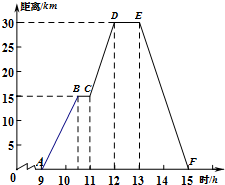 小强骑自行车去郊游,9时出发,15时返回.右图表示他距家的距离y(千米)与相应的时刻x(时)之间的函数关系的图象.根据这个图象,小强14时距家的距离是( )
小强骑自行车去郊游,9时出发,15时返回.右图表示他距家的距离y(千米)与相应的时刻x(时)之间的函数关系的图象.根据这个图象,小强14时距家的距离是( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com