
【题目】如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为 . 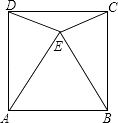
【答案】150°
【解析】解:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠ADC=∠BCD=90°,AB=BC=CD=DA,
∵△ABE是等边三角形,
∴AB=AE=BE,∠BAE=∠ABE=60°,
∴AE=AD=BE=BC,∠DAE=∠CBE=30°,
∴∠ADE=∠BCE= ![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠EDC=∠ECD=15°,
∴∠CED=180°﹣15°﹣15°=150°.
所以答案是:150°.
【考点精析】本题主要考查了等边三角形的性质和正方形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD的内部,延长AF交CD于点G.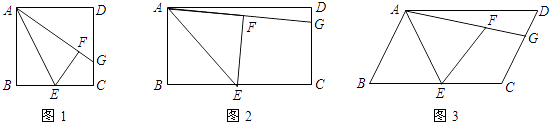
(1)猜想并证明线段GF与GC的数量关系;
(2)若将图1中的正方形改成矩形,其它条件不变,如图2,那么线段GF与GC之间的数量关系是否改变?请证明你的结论;
(3)若将图1中的正方形改成平行四边形,其它条件不变,如图3,那么线段GF与GC之间的数量关系是否会改变?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
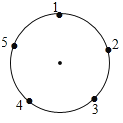
【题目】如图是一个圆,一只电子跳蚤在标有五个数字的点上跳跃,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若跳蚤从2这点开始跳,则经2017次跳后它停在数____对应的点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE. 
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com