Question

【题目】如图，在正方形ABCD中，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在正方形ABCD的内部，延长AF交CD于点G．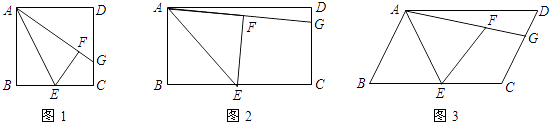

（1）猜想并证明线段GF与GC的数量关系；
（2）若将图1中的正方形改成矩形，其它条件不变，如图2，那么线段GF与GC之间的数量关系是否改变？请证明你的结论；
（3）若将图1中的正方形改成平行四边形，其它条件不变，如图3，那么线段GF与GC之间的数量关系是否会改变？请证明你的结论．

Answer 1

【答案】
（1）

解：FG=CG，理由如下：

∵E是BC的中点

∴BE=CE

∵将△ABE沿AE折叠后得到△AFE

∴BE=EF，

∴EF=EC；

同样，在折叠中，∠B=∠EFA=90°

又∵∠C=∠B，∠EFG=∠EFA

∴∠C=∠EFG=90°

∵EG=EG，

∴△ECG≌△EFG

∴FG=CG

（2）

解：不会改变．

证明：连接EG

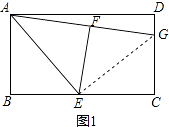
∵E是BC的中点

∴BE=CE

∵将△ABE沿AE折叠后得到△AFE

∴BE=EF，

∴EF=EC；

同样，在折叠中，∠B=∠EFA=90°

又∵∠C=∠B，∠EFG=∠EFA

∴∠C=∠EFG=90°

∵EG=EG，

∴△ECG≌△EFG

∴FG=CG；

（3）

解：不会改变．

证明：连接EG、FC

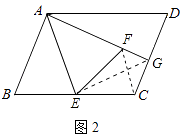
∵E是BC的中点

∴BE=CE

∵将△ABE沿AE折叠后得到△AFE

∴BE=EF，∠B=∠AFE

∴EF=EC

∴∠EFC=∠ECF

∵矩形ABCD改为平行四边形

∴∠B=∠D

∵∠ECD=180°﹣∠D，∠EFG=180°﹣∠AFE=180°﹣∠B=180°﹣∠D

∴∠ECD=∠EFG

∴∠GFC=∠GFE﹣∠EFC=∠ECG﹣∠ECF=∠GCF

∴∠GFC=∠GCF

∴△ECG≌△EFG

∴FG=CG

即（1）中的结论仍然成立

【解析】（1）判定直角三角形△ECG和△EFG全等，和全等三角形对应边相等的性质；（2）判定直角三角形△ECG和△EFG全等，和全等三角形对应边相等的性质；（3）判定△ECG和△EFG全等，根据全等三角形对应边相等性质即可证明．