
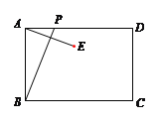
【题目】如图,已知矩形ABCD中,AB=4,动点P从点A出发,沿AD方向以每秒1个单位的速度运动,连接BP,作点A关于直线BP的对称点E,设点P的运动时间为t(s).在动点P在射线AD上运动的过程中,则使点E到直线BC的距离等于3时对应的t的值为______.
【答案】![]() 或
或![]()
【解析】
分两种情况:①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,AN=BM=![]() ,得出△BME∽△ENP,得出
,得出△BME∽△ENP,得出![]() ,求出NP=
,求出NP=![]() ,即可得出结果;
,即可得出结果;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,则BH=3,BE=AB=4,AH=AB+BH=7,HE=![]() ,得△AHE∽△PAB,得出
,得△AHE∽△PAB,得出![]() ,即可得出结果.
,即可得出结果.
①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,如图1所示:

则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,
在Rt△EBM中,AN=BM=![]() ,
,
∵点A、E关于直线BP对称,
∴∠PEB=∠PAB=90°,
∵∠ENP=∠EMB=∠PEB=90°,
∴∠PEN=∠EBM,
∴△BME∽△ENP,
∴![]() ,即
,即![]() ,
,
∴NP=![]() ,
,
∴t=AP=AN-NP=;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,如图2所示:
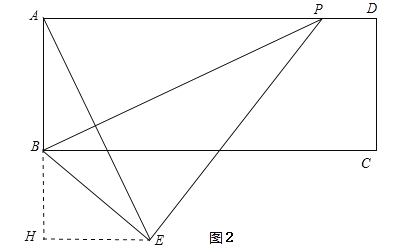
则BH=3,BE=AB=4,AH=AB+BH=7,
在Rt△BHE中,HE=![]() ,
,
∵∠PAB=∠BHE=90°,AE⊥BP,
∴∠APB+∠EAP=∠HAE+∠EAP=90°,
∴∠HAE=∠APB,
∴△AHE∽△PAB,
∴![]() ,即
,即![]() ,
,
解得:t=AP=4![]() ,
,
综上所述,t=![]() 或4
或4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
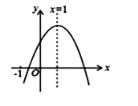
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②4a+2b+c>0;③2a+b=0;④b2>4ac; ⑤ 3a+c>0.其中正确的结论的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
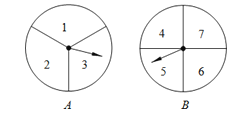
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
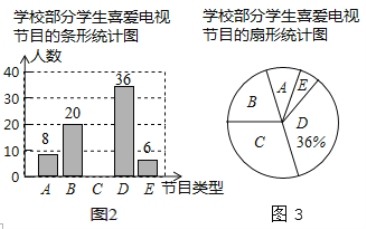
【题目】为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图1所示),并根据调查结果绘制了图2、图3两幅统计图(均不完整),请根据统计图解答下列问题.
(1)本次接受问卷调查的学生有________名.
(2)补全条形统计图.
(3)扇形统计图中B类节目对应扇形的圆心角的度数为________.
(4)该校共有2000名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
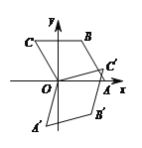
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=4,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A. (2![]() ,﹣2
,﹣2![]() )B. (
)B. (![]() ,-
,-![]() )C. (2,﹣2)D. (
)C. (2,﹣2)D. (![]() ,-
,-![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是( )

A. AB=CD,AB⊥CDB. AB=CD,AD=BC
C. AB=CD,AC⊥BDD. AB=CD,AD∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
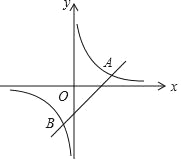
【题目】如图,已知一次函数y=x﹣2与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象与 x 轴交于 A(﹣3,0),B(1,0)两点,与 y 轴交于点C.
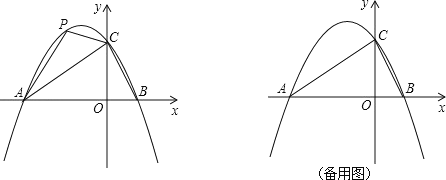
(1)求这个二次函数的关系解析式 ,x 满足什么值时 y﹤0 ?
(2)点 p 是直线 AC 上方的抛物线上一动点,是否存在点 P,使△ACP 面积最大?若存在,求出点 P的坐标;若不存在,说明理由
(3)点 M 为抛物线上一动点,在 x 轴上是否存在点 Q,使以 A、C、M、Q 为顶点的四边形是平行四边形?若存在,直接写出点 Q 的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com