
 如图,直线AB:y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,直线上一动点P以1cm/s的速度由点A向终点B运动,设运动时间为t(s).
如图,直线AB:y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,直线上一动点P以1cm/s的速度由点A向终点B运动,设运动时间为t(s).分析 (1)根据y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,于是令x=0,y=0,解方程即可得到结论;
(2)根据勾股定理得到AB的长,由三角形的面积公式得到OA•OB=AB•OP,代入数据即可得到结论;
(3)①根据平行线分线段成比例定理列比例式求得t,②根据AP=OA,求得t,③根据相似三角形的性质即可得到t.
解答 解:(1)在y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$中,令x=0,得y=$\sqrt{3}$,y=0,得x=$\sqrt{2}$,
∴A的坐标为($\sqrt{2}$,0),点B的坐标为(0,$\sqrt{3}$);
故答案为:($\sqrt{2}$,0),(0,$\sqrt{3}$);
(2)当OP⊥AB时,OP的距离最短,
∵OA=$\sqrt{2}$,OB=$\sqrt{3}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{5}$,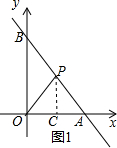
∵S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OP,
∴OP=$\frac{OA•OB}{AB}$=$\frac{\sqrt{30}}{5}$;
(3)①如图1,当OP=AP,过P作PC⊥OA于C,
∴AC=0C,
∴PC∥OB,
∴$\frac{AP}{AB}=\frac{AC}{AO}$=$\frac{1}{2}$,
∴t=$\frac{\sqrt{5}}{2}$,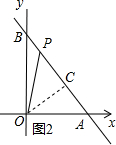
②当AP=OA时,
即t=$\sqrt{2}$,
③如图2,当OA=OP时,过O作OC⊥AB于C,
∴∠ACO=∠AOB=90°,
∵∠OAB=∠AOC,
∴△AOC∽△AOB,
∴$\frac{AO}{AB}=\frac{AC}{OA}$,
∴$\frac{\sqrt{2}}{\sqrt{5}}=\frac{AC}{\sqrt{2}}$,
∴AC=$\frac{2\sqrt{5}}{5}$,
∴AP=t=2AC=$\frac{4\sqrt{5}}{5}$.
综上所述:当t=$\frac{\sqrt{5}}{2}$,$\sqrt{2}$,$\frac{4\sqrt{5}}{5}$时,△OAP为等腰三角形.
点评 本题考查了一次函数与坐标轴的交点,三角形的面积公式,相似三角形的判定和性质,等腰三角形的性质,正确的作出图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 依次连接四边形四边中点所组成的图形是矩形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
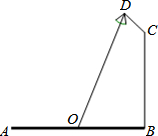 如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.
如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
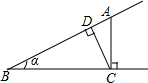 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )| A. | $\frac{CD}{AC}$ | B. | $\frac{BC}{AB}$ | C. | $\frac{BD}{BC}$ | D. | $\frac{AD}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com