练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．下列命题中，是真命题的是（　　）
    A．相等的圆心角所对的弧相等，所对的弦也相等
    B．平分弦的直径垂直于弦
    C．依次连接四边形四边中点所组成的图形是矩形
    D．一组邻边相等的平行四边形是菱形

    分析 根据圆心角、弧、弦的关系对A进行判断；根据垂径定理的推论对B进行判断；根据三角形中位线性质和平行四边形的判定方法对C进行判断；根据菱形的判定方法对D进行判断．

    解答 解：A、在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等，所以A选项错误；
    B、平分弦（非直径）的直径垂直于弦，所以B选项错误；
    C、依次连接四边形四边中点所组成的图形是平行四边形，所以C选项错误；
    D、一组邻边相等的平行四边形是菱形，所以D选项正确．
    故选D．

    点评 本考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式． 有些命题的正确性是用推理证实的，这样的真命题叫做定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．（1）（$\sqrt{3}$+$\sqrt{6}$）2
    （2）$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$
    （3）$\sqrt{18}+{（\sqrt{2}+1）^{-1}}+{（-2）^{-2}}$
    （4）$\frac{2}{3}\sqrt{3\frac{3}{4}}×（-9\sqrt{45}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

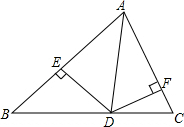    8．如图，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，则有下列结论：
    （1）△ADE≌△ADF；（2）△BDE≌△CDF；（3）△ABD≌△ACD；（4）AE=AF；（5）BE=CF；（6）BD=CD；（7）∠ADE=∠ADF
    正确的有①④⑦（只填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．若$\sqrt{{（a-4）}^{2}}$=a-4，则a的取值范围是（　　）
    A．a＜4B．a≤4C．a＞4D．a≥4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．一圆锥的侧面展开后是扇形，该扇形的圆心角为120°，半径为6cm，则此圆锥的底面圆的面积为4πcm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．2015年8月5日，河南省长恒县第一中学发布了体育看台建设项目施工招标的公告，该看台的部分侧面示意图如图所示，该看台每个台阶的高度都相等，线段MN表示的是看台上方的遮阳板．已知∠ACE=30°，CD=2$\sqrt{3}$m，DE=BN=1m，∠E=∠ADE=90°，MN∥CE．
    （1）求CF的高度；
    （2）若MN=$\frac{4\sqrt{3}-3}{2}$m，求点M到点C的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．抛物线y=-2x2+4x+1如图所示，作该抛物线关于点O对称的图形，得到一条新的抛物线，则新抛物线的解析式为y=2（x+12）-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，直线AB：y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点，直线上一动点P以1cm/s的速度由点A向终点B运动，设运动时间为t（s）．
    （1）点A的坐标为（$\sqrt{2}$，0）；点B的坐标为（0，$\sqrt{3}$）；
    （2）求OP的最短距离；
    （3）是否存在t的值，使△OAP为等腰三角形？若存在，直接写出满足条件的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知二次函数y=k（x+1）（x-$\frac{3}{k}$）的图象与x轴交于点A，B，与y轴交于点C．
    （1）写出点C的坐标；
    （2）若△ABC为等腰三角形，求k的值．

    查看答案和解析>>

    同步练习册答案