Question

2．2015年8月5日，河南省长恒县第一中学发布了体育看台建设项目施工招标的公告，该看台的部分侧面示意图如图所示，该看台每个台阶的高度都相等，线段MN表示的是看台上方的遮阳板．已知∠ACE=30°，CD=2$\sqrt{3}$m，DE=BN=1m，∠E=∠ADE=90°，MN∥CE．
（1）求CF的高度；
（2）若MN=$\frac{4\sqrt{3}-3}{2}$m，求点M到点C的距离．

Answer 1

分析 （1）RT△ACD中，由∠ACD=30°知AC=2AD，再根据勾股定理可求得AD的长度，除以台阶数即可得；
（2）过点M作MP⊥CE于点P，连接MC，由题意可知MP=NE=AD+BN，CP=CE-PE=CE-MN，在RT△PCM中根据勾股定理可得MC长度．

解答 解：（1）在RT△ACD中，∵∠ACD=30°，
∴AC=2AD，
又∵AC²=AD²+CD²，且CD=2$\sqrt{3}$，
∴4AD²=AD²+12，解得：AD=2，
由图可知，共有5个台阶，
故CF=$\frac{1}{4}$AD=0.4m；
（2）过点M作MP⊥CE于点P，连接MC，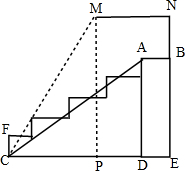

∴∠MPE=∠E=90°，
∴MP∥NE，
又∵MN∥CE，
∴四边形MNEP为矩形，
∴MP=NE=AB+BN=AD+BN=3m，
CP=CE-PE=CE-MN=2$\sqrt{3}$+1-$\frac{4\sqrt{3}-3}{2}$=$\frac{5}{2}$m，
在RT△PCM中，∵MC²=MP²+CP²，
∴MC=$\sqrt{{3}^{2}+（\frac{5}{2}）^{2}}$=$\frac{\sqrt{61}}{2}$，
故点M到点C的距离为$\frac{\sqrt{61}}{2}$m．

点评 本题主要考查勾股定理及矩形的判定与性质，做垂直构建直角三角形根据勾股定理求斜边长度是切入点，根据矩形性质得出直角三角形直角边长是关键．