
分析 (1)计算自变量为0时的函数值即可得到C点坐标;
(2)先通过解方程k(x+1)(x-$\frac{3}{k}$)=0得点A、B坐标,讨论:若k>0,当CA=CB,则OA=OB;当AB=AC;当BA=BC时;若k<0时,AB=AC,利用两点间的距离公式分别得到关于k的方程,然后解方程求出对应的k的值.
解答 解:(1)当x=0时,y=k(x+1)(x-$\frac{3}{k}$)=k•(-$\frac{3}{k}$)=-3,
所以C点坐标为(0,-3);
(2)当y=0时,k(x+1)(x-$\frac{3}{k}$)=0,解得x1=-1,x2=$\frac{3}{k}$,
设A(-1,0),B($\frac{3}{k}$,0),
AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$
若k>0,
当CA=CB,则OA=OB,即$\frac{3}{k}$=1,解得k=3;
当AB=AC,解$\frac{3}{k}$+1=$\sqrt{10}$,解得k=$\frac{\sqrt{10}+1}{3}$;
当BA=BC时,即$\frac{3}{k}$+1=$\sqrt{{3}^{2}+(\frac{3}{k})^{2}}$,解得k=$\frac{3}{4}$;
若k<0时,AB=AC,即-1-$\frac{3}{k}$=$\sqrt{10}$,解得k=-$\frac{\sqrt{10}-1}{3}$,
综上所述,k的值为3或$\frac{3}{4}$或-$\frac{\sqrt{10}-1}{3}$或$\frac{\sqrt{10}+1}{3}$.
点评 本题考查了抛物线与x轴的交点问题:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了分类讨论的思想和等腰三角形的性质.


科目:初中数学 来源: 题型:选择题
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 依次连接四边形四边中点所组成的图形是矩形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
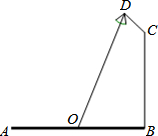 如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.
如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
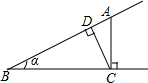 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )| A. | $\frac{CD}{AC}$ | B. | $\frac{BC}{AB}$ | C. | $\frac{BD}{BC}$ | D. | $\frac{AD}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象,在第一象限交于点A,连接OA,若S△AOB:S△BOC=1:2,则k的值为3.
如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象,在第一象限交于点A,连接OA,若S△AOB:S△BOC=1:2,则k的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com