
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【答案】
(1)解:设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得: ![]() ,
,
解得: ![]() ,
,
答:A、B两种型号电风扇的销售单价分别为250元、210元
(2)解:设采购A种型号电风扇a台,则采购B种型号电风扇(30﹣a)台.
依题意得:200a+170(30﹣a)≤5400,
解得:a≤10.
答:超市最多采购A种型号电风扇10台时,采购金额不多于5400元
(3)解:依题意有:(250﹣200)a+(210﹣170)(30﹣a)=1400,
解得:a=20,
∵a≤10,
∴在(2)的条件下超市不能实现利润1400元的目标
【解析】(1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号5台B型号的电扇收入1800元,4台A型号10台B型号的电扇收入3100元,列方程组求解即可;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台,根据金额不多余5400元,列不等式求解即可得出答案;
(3)设利润为1400元,列方程求出a的值为20,不符合(2)的条件,可知不能实现目标.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
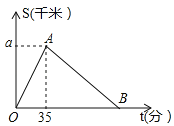
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回中点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=100°,∠ACB=40°,∠ABC的平分线BD交AC于点D,∠ACB的平分线CP交BD于点D.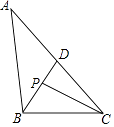
(1)BD与AC的位置关系是 .
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )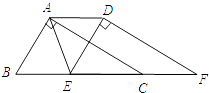
A.AD∥BE,AD=BE
B.∠ABE=∠DEF
C.ED⊥AC
D.△ADE为等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l经过点(0,﹣2),且直线l∥x轴.若直线l与二次函数y=3x2+a的图象交于A,B两点,与二次函数y=﹣2x2+b的图象交于C,D两点,其中a,b为整数.若AB=2,CD=4.则b﹣a的值为( )
A.9B.11C.16D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.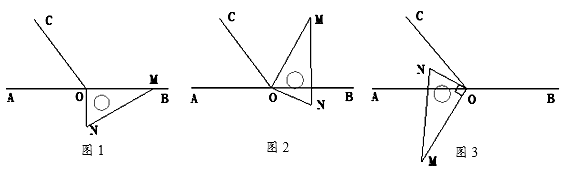
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.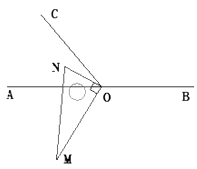
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com