
【题目】某数学兴趣小组对该校学生一天的零用钱数额(单位:元)进行了随机抽样调查,现将抽样数据分成五组(第一组:0~1元,含0元,1元;第二组:1元~2元,含2元;第三组:2元~3元,含3元;第四组:3元~4元,含4元;第五组:4元~5元,含5元),其统计图如图所示.第一组的人数、频率分别为2,0.04,第二、三、五组的频率分别为0.24,0.20,0.36. 
(1)该数学兴趣小组随机抽样了多少名学生?
(2)请你通过计算后,补全统计图.
(3)如果我们在校园中随机抽查一名学生,一天的零用钱在2元以上(不含2元)的学生被抽到的概率是多少?
【答案】
(1)解:2÷0.04=50(名)
(2)解:第四组的频率为:1﹣0.04﹣0.24﹣0.20﹣0.36=0.16;
第二组人数为:50×0.24=12(名),
第三组人数为:50×0.20=10(名),
第五组人数为:50×0.36=18(名),
第四组人数为:50×0.16=8(名);
补全统计图如图报示:
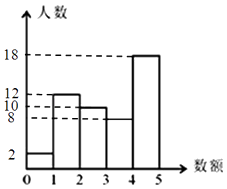
(3)解:一天的零用钱在2元以上的频率=0.20+0.16+0.36=0.72,
所以在校园中随机抽查一名学生,一天的零用钱在2元以上的概率为0.72
【解析】(1)根据第一组的人数、频率进行解答;(2)根据第四组的频率解答;(3)由概率的定义解答.
【考点精析】本题主要考查了频数分布直方图和概率公式的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能正确解答此题.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程![]() 的两个根,点C在
的两个根,点C在![]() 轴正半轴上,且OB=2OC.
轴正半轴上,且OB=2OC.
(1)求A、B、C三点坐标;
(2)将△OBC绕点C顺时针旋转90°后得到![]() ,求直线
,求直线![]() 的表达式.
的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(图1),后人称其为“赵爽弦图”,由弦图变化得到图2,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=12,则S2的值为_______.
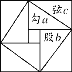
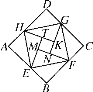
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是96分,请问小红在竞赛中答对了多少题?
(2)小明也参加了竞赛,考完后他说:“这次竟赛中我一定能拿到110分.”请问小明有没有可能拿到110分?试用方程的知识来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“WJ一号”水稻种子,当年种植,当年收割,当年出水稻产量,(以后每年要出产量还需重要新种植),某村2014、2015、2016年连续尝试种植了此水稻种子.2015年和2016年种植面积都比上年减少相同的数量,若2016年平均每公顷水稻产量比2015年增加的百分数是2015年比2014年增加的百分数的1.25倍,2016年比2014年种植面积减少的百分数与2016年水稻总产量比2014年增加的百分数相同,都等于2015年比上年平均每公顷水稻产量增加的百分数.
(1)求2016年平均每公顷水稻产量比2015年增加的百分数;
(2)求2015年这种水稻总产量比上年增加的百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方体六个面展开如图所示,六个面分别用字母A、B、C、D、E、F表示,已知:A=x2﹣4xy+3y2,B=![]() (C﹣A),C=3x2﹣2xy﹣y2,E=B﹣2C,若正方体相对的两个面上的多项式的和相等,求D、F.(用含x,y的多项式表示)
(C﹣A),C=3x2﹣2xy﹣y2,E=B﹣2C,若正方体相对的两个面上的多项式的和相等,求D、F.(用含x,y的多项式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC.点E是y轴上任意一点记点E为(0,n).
(1)求直线BC的关系式;
(2)连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形DEFG的顶点F落在△ABC的边上?若存在,求出所有的n值并直接写出此时正方形DEFG与△ABC重叠部分的面积;若不存在,请说明理由.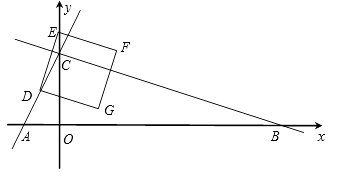
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com