
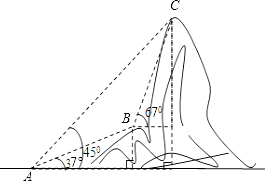
【题目】如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() ,sin67°≈
,sin67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() )
)
【答案】解:如图,过点C作经过点A的水平直线的垂线,垂足为点D,CD交过点B的水平直线于点E,
过点B作BF⊥AD于点F,则CD=330米,
∵∠CAD=45°
∴∠ACD=45°
∴AD=CD=330米,
设AF=4x,则BF=AFtan37°≈4x ![]() =3x(米)
=3x(米)
FD=(330﹣4x)米,
由四边形BEDF是矩形可得:BE=FD=(330﹣4x)米,ED=BF=3x米,
∴CE=CD﹣ED=(330﹣3x)米,
在Rt△BCE中,CE=BEtan67°,
∴330﹣3x=(330﹣4x)× ![]() ,
,
解得x=70,
∴CE=330﹣3×70=120(米),
∴BC= ![]() =
= ![]() ≈130(米)
≈130(米)
答:电缆BC长至少130米.
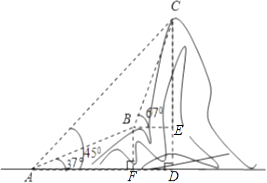
【解析】过点C作经过点A的水平直线的垂线,垂足为点D,CD交过点B的水平直线于点E,过点B作BF⊥AD于点F,根据题意求出AD=CD,设AF=4x,利用正切的定义用x表示出BF,求出CE,根据正弦的定义列式计算即可.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.


科目:初中数学 来源: 题型:
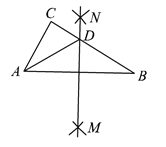
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为16,△ABC的周长28,则AB为___________.
AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为16,△ABC的周长28,则AB为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
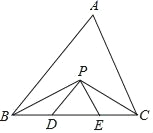
【题目】如图,在△ABC中,BC=8cm,∠BPC=118°,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是_____cm,∠DPE=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图像经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当
2≤x≤3时,y2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古运河是扬州的母亲河.为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲: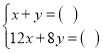 ;乙:
;乙: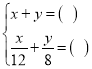 .
.
根据甲、乙两名问学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示______,y表示_______;
乙:x表示_____,y表示_______.
(2)求A、B两工程队分别整治河道多少米.(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小赵为班级购买笔记本作为晚会上的奖品回来时向生活委员交账说:“一共买了![]() 本,有两种规格,单价分别为
本,有两种规格,单价分别为![]() 元和
元和![]() 元去时我领了
元去时我领了![]() 元,现在找回
元,现在找回![]() 元”生活委员算了一下,认为小赵搞错了.
元”生活委员算了一下,认为小赵搞错了.
(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起 当做找回的钱给了生活委员.如果设购买单价为![]() 元的笔记本
元的笔记本![]() 本,试用含
本,试用含![]() 的代数式表示小赵零用钱的数目: 元
的代数式表示小赵零用钱的数目: 元
(3)如果小赵的零用钱数目是整数,且少于![]() 元,试求出小赵零用钱的数目.
元,试求出小赵零用钱的数目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张看上去无差别的卡片,上面分别写着0,π, ![]() ,
, ![]() ,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题: 某校为美化校园,计划对一些区域进行绿化,安排了甲、乙两个工程队完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且两队在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com