
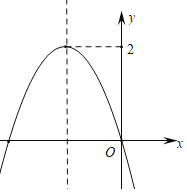
【题目】二次函数y=ax2+bx的图象如图所示,若关于x的一元二次方程ax2+bx+k-1=0没有实数根,则k的取值范围为______.
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=-![]() x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
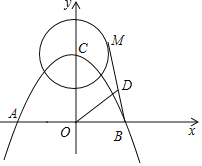
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为![]() 米,中午
米,中午![]() 时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方
时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方![]() 米处再建一幢新楼. 已知该地区冬天中午
米处再建一幢新楼. 已知该地区冬天中午![]() 时阳光从正南方照射,并且光线与水平线的夹角最小为
时阳光从正南方照射,并且光线与水平线的夹角最小为![]() °,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.
°,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
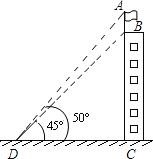
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2100元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
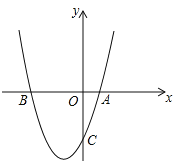
(1)求该抛物线的解析式;
(2)若点![]() 为线段
为线段![]() 上一动点,试求
上一动点,试求![]() 的最小值;
的最小值;
(3)点![]() 是
是![]() 轴左侧的抛物线上一动点,连接
轴左侧的抛物线上一动点,连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com