
【题目】如图,在平面直角坐标系中,二次函数y=-![]() x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
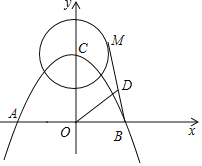
科目:初中数学 来源: 题型:
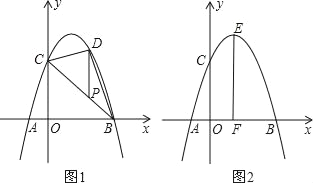
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
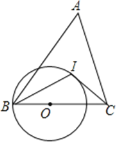
【题目】如图,△ABC中,AC=BC,点I是△ABC的内心,点O在边BC上,以点O为圆心,OB长为半径的圆恰好经过点I,连接CI,BI.
(1)求证:CI是⊙O的切线;
(2)若AC=BC=5,AB=6,求BI的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是⊙O的直径,点E是弧BF的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
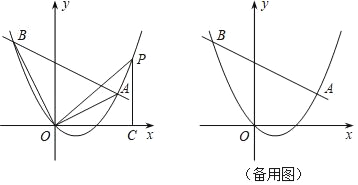
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
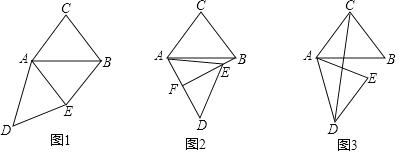
【题目】已知:在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转(旋转角度小于180°),得到△ADE,点B的对应点为点D,点C的对应点为点E.
(1)如图1,连接BE,若∠DAB+∠ACB=180°,请判断四边形AEBC的形状,并说明理由;
(2)如图2,设BE的延长线与AD交于点F,若AF=FD,求∠BAD的度数;
(3)如图3,连接CD,若∠CAE=∠ACB,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工厂开发新产品,需要用甲、乙两种化工原料配制A、B两种产品共40桶,技术员到仓库进行准备,发现库存甲种原料300升,乙种原料170升,已知配制A、B两种产品每桶需要的甲、乙两种原料数如下表:

若配制一桶A产品需要![]() 小时,配制一桶B产品需要
小时,配制一桶B产品需要![]() 小时,求完成这两种产品的开发最少需要多少时间?
小时,求完成这两种产品的开发最少需要多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知ABCD中,以AB为斜边在ABCD内作等腰直角△ABE,且AE=AD,连接DE,过E作EF⊥DE交AB于F交DC于G,且∠AEF=15°
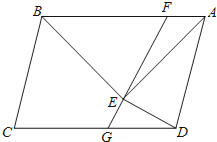
(1)若EF=![]() ,求AB的长.
,求AB的长.
(2)求证:2GE+EF=AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com