
【题目】AB是⊙O的直径,点E是弧BF的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
【答案】![]()
【解析】
连接OE,OF、EF,根据切线的性质和含30°角的直角三角形的性质求得CE的长,再由已知条件求得AE=CE=![]() ,然后在直角三角形ADE中求得AD和DE,再根据三角形的面积公式和扇形的面积公式求阴影部分的面积即可.
,然后在直角三角形ADE中求得AD和DE,再根据三角形的面积公式和扇形的面积公式求阴影部分的面积即可.
解:连接OE,OF、EF,
∵DE是切线,
∴OE⊥DE,
∵∠C=30°,OB=OE=2,
∴∠EOC=60°,OC=2OE=4,
∴CE=OC×sin60°=4×sin60°=![]() ,
,
∵点E是弧BF的中点,
∴∠EAB=∠DAE=30°,∠DAO=60°,
∴F,E是半圆弧的三等分点,
∴∠EOF=∠EOB=∠AOF=60°,
∴OE∥AD,
∴∠ADC=90°,
∵∠EAB=∠C=30°
∴AE=CE=![]() ,
,
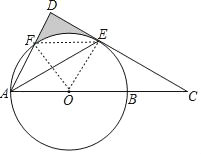
∵∠EAD=30°,∠ADC=90°,
∴DE=![]() ,
,
∴AD=DE×tan60°=![]() ,
,
∴S△ADE=![]()
∵△FOE和△AEF同底等高,
∴△FOE和△AEF面积相等,
∴图中阴影部分的面积为:S△ADE﹣S扇形FOE=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】涌泉镇是中国无核蜜桔之乡,已知某蜜桔种植大户冯大爷的蜜桔成本为2元/千克,如果在未来90天蜜桔的销售单价p(元/千克)与时间t(天)之间的函数关系式为p=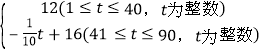 ,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
时间t/天 | 1 | 10 | 20 | 40 | 70 | 90 |
日销售量y/千克 | 105 | 150 | 200 | 300 | 450 | 550 |
(1)求y与t之间的函数表达式;
(2)在未来90天的销售中,预测哪一天的日销售利润最大?最大日销售利润为多少元?
(3)在实际销售的后50天中,冯大爷决定每销售1千克蜜桔就捐赠n元利润(n<5)给留守儿童作为助学金,销售过程中冯大爷发现,恰好从第51天开始,和前一天相比,扣除捐赠后的日销售利润逐日减少,请求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了5次射击训练,平均成绩为9环,且前4次的成绩(单位:环)依次为:8,10,9,10.
(1)求甲第5次的射击成绩与这5次射击成绩的方差;
(2)乙在相同情况下也进行了5次射击训练,平均成绩为9环,方差为0.9环,请问甲和乙哪个的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
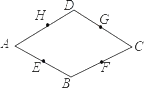
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=-![]() x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
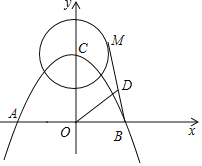
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为![]() 米,中午
米,中午![]() 时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方
时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方![]() 米处再建一幢新楼. 已知该地区冬天中午
米处再建一幢新楼. 已知该地区冬天中午![]() 时阳光从正南方照射,并且光线与水平线的夹角最小为
时阳光从正南方照射,并且光线与水平线的夹角最小为![]() °,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.
°,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
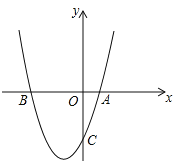
(1)求该抛物线的解析式;
(2)若点![]() 为线段
为线段![]() 上一动点,试求
上一动点,试求![]() 的最小值;
的最小值;
(3)点![]() 是
是![]() 轴左侧的抛物线上一动点,连接
轴左侧的抛物线上一动点,连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com