
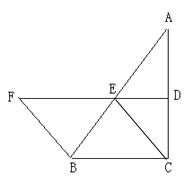
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() 分别是
分别是![]() 的中点,延长
的中点,延长![]() 到
到![]() ,使
,使![]() .
.
(1)证明:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 是菱形,则
是菱形,则![]() 应为多少度.
应为多少度.
【答案】(1)见解析;(2)![]()
【解析】
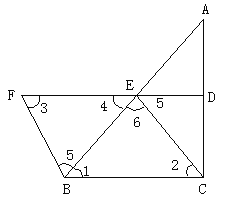
(1)根据直角三角形斜边上的中线等于斜边的一半可得CE =BE=![]() AB,从而得到BF=CE,根据等边对等角可得∠1=∠2,∠3=∠4,然后由三角形的中位线得出ED∥BC,由平行线的性质求出∠1=∠4=∠2=∠3,则∠5=∠6,易得CE∥BF,然后利用两组对边分别平行的四边形是平行四边形证明;
AB,从而得到BF=CE,根据等边对等角可得∠1=∠2,∠3=∠4,然后由三角形的中位线得出ED∥BC,由平行线的性质求出∠1=∠4=∠2=∠3,则∠5=∠6,易得CE∥BF,然后利用两组对边分别平行的四边形是平行四边形证明;
(2)根据菱形的四条边都相等可得BC=CE=![]() AB,然后根据含30°角的直角三角形的性质解答.
AB,然后根据含30°角的直角三角形的性质解答.
(1)证明:∵![]() 是直角三角形
是直角三角形
且![]() 是
是![]() 中点,
中点,
∴![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]() ;
;
∵![]() 是
是![]() 中点,
中点,
∴![]() ,∴
,∴![]()
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
(2)解:∵![]() 是菱形,∴
是菱形,∴![]() ,
,
∵![]() 是直角三角形,
是直角三角形,
∴![]() .
.
故答案为:(1)见解析;(2)![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】问题提出:求n个相同的长方体(相邻面的面积不相同)摆放成一个大长方体的表面积.
问题探究:探究一:
为了研究这个问题,同学们建立了如下的空间直角坐标系:空间任意选定一点O,以点O为端点,作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴,统称为坐标轴,它们的方向分别为ox(水平向前)、oy(水平向右)、oz(竖直向上)方向.
将相邻三个面的面积记为S1、S2、S3,且S1<S2<S3的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体S1所在的面与x轴垂直,S2所在的面与y轴垂直,S3所在的面与z轴垂直,如图1所示.
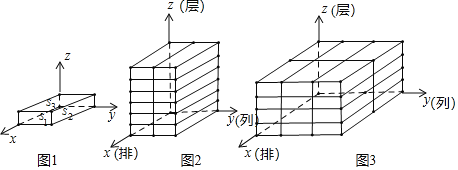
若将x轴方向表示的量称为几何体码放的排数,y轴方向表示的量称为几何体码放的列数,z轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标系内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作(1,2,6),如图3的几何体码放了2排3列4层,用有序数组记作(2,3,4).这样我们就可用每一个有序数组(x,y,z)表示一种几何体的码放方式.
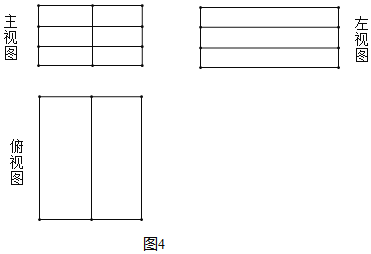
问题一:如图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为______.
组成这个几何体的单位长方体的个数为______个.
探究二:
为了探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),同学们针对若干个单位长方体进行码
放,制作了下列表格
几何体 有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
(1,1,1) | 1 | 2 | 2 | 2 | 2S1+2S2+2S3 |
(1,2,1) | 2 | 4 | 2 | 4 | 4S1+2S2+4S3 |
(3,1,1) | 3 | 2 | 6 | 6 | 2S1+6S2+6S3 |
(2,1,2) | 4 | 4 | 8 | 4 | 4S1+8S2+4S3 |
(1,5,1) | 5 | 10 | 2 | 10 | 10S1+2S2+10S3 |
(1,2,3) | 6 | ||||
…… | …… | …… | …… | …… | …… |
问题二:请将上面表格补充完整:当单位长方体的个数是6时,表面上面积为S1的个数是______.
表面上面积为S2的个数是______;表面上面积为S3的个数是______;表面积为______.
问题三:根据以上规律,请写出有序数组(x,y,z)的几何体表面积计算公式S(x,y,z)=______(用x、y、z、S1、S2、S3表示)
探究三:
同学们研究了当S1=2,S2=3,S3=4时,用3个单位长方体码放的几何体中,有三种码放的方法,有序数组分别为(1,1,3),(1,3,1),(3,1,1).而S(1,1,3)=38,S(1,3,1)=42,S(3,1,1)=46.容易发现个数相同的长方体,由于码放的方法不同,组成的几何体的表面积就不同.
拓展应用:
要将由20个相同的长方体码放的几何体进行打包,其中每个长方体的长是8,宽是5,高是6.为了节约外包装材料,请直接写出使几何体表面积最小的有序数组,并写出这个最小面积(不需要写解答过程).(缝隙不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
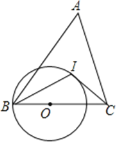
【题目】如图,△ABC中,AC=BC,点I是△ABC的内心,点O在边BC上,以点O为圆心,OB长为半径的圆恰好经过点I,连接CI,BI.
(1)求证:CI是⊙O的切线;
(2)若AC=BC=5,AB=6,求BI的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
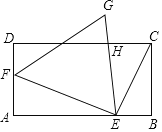
【题目】如图,已知矩形ABCD中,BC=2cm,AB=2![]() cm,点E在边AB上,点F在边AD上,点E由A向B运动,连结EC、EF,在运动的过程中,始终保持EC⊥EF,△EFG为等边三角形.
cm,点E在边AB上,点F在边AD上,点E由A向B运动,连结EC、EF,在运动的过程中,始终保持EC⊥EF,△EFG为等边三角形.
(1)求证△AEF∽△BCE;
(2)设BE的长为xcm,AF的长为ycm,求y与x的函数关系式,并写出线段AF长的范围;
(3)若点H是EG的中点,试说明A、E、H、F四点在同一个圆上,并求在点E由A到B运动过程中,点H移动的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是⊙O的直径,点E是弧BF的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
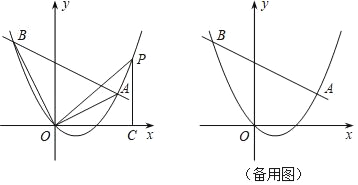
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工厂开发新产品,需要用甲、乙两种化工原料配制A、B两种产品共40桶,技术员到仓库进行准备,发现库存甲种原料300升,乙种原料170升,已知配制A、B两种产品每桶需要的甲、乙两种原料数如下表:

若配制一桶A产品需要![]() 小时,配制一桶B产品需要
小时,配制一桶B产品需要![]() 小时,求完成这两种产品的开发最少需要多少时间?
小时,求完成这两种产品的开发最少需要多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com