
【题目】问题提出:求n个相同的长方体(相邻面的面积不相同)摆放成一个大长方体的表面积.
问题探究:探究一:
为了研究这个问题,同学们建立了如下的空间直角坐标系:空间任意选定一点O,以点O为端点,作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴,统称为坐标轴,它们的方向分别为ox(水平向前)、oy(水平向右)、oz(竖直向上)方向.
将相邻三个面的面积记为S1、S2、S3,且S1<S2<S3的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体S1所在的面与x轴垂直,S2所在的面与y轴垂直,S3所在的面与z轴垂直,如图1所示.
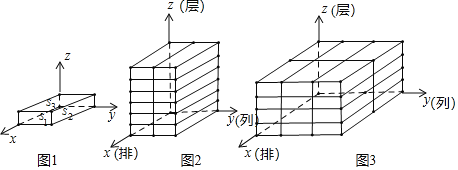
若将x轴方向表示的量称为几何体码放的排数,y轴方向表示的量称为几何体码放的列数,z轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标系内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作(1,2,6),如图3的几何体码放了2排3列4层,用有序数组记作(2,3,4).这样我们就可用每一个有序数组(x,y,z)表示一种几何体的码放方式.
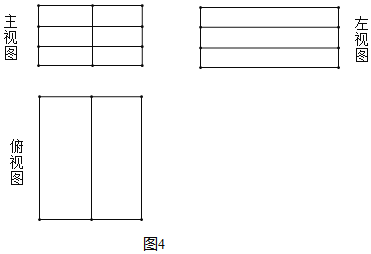
问题一:如图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为______.
组成这个几何体的单位长方体的个数为______个.
探究二:
为了探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),同学们针对若干个单位长方体进行码
放,制作了下列表格
几何体 有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
(1,1,1) | 1 | 2 | 2 | 2 | 2S1+2S2+2S3 |
(1,2,1) | 2 | 4 | 2 | 4 | 4S1+2S2+4S3 |
(3,1,1) | 3 | 2 | 6 | 6 | 2S1+6S2+6S3 |
(2,1,2) | 4 | 4 | 8 | 4 | 4S1+8S2+4S3 |
(1,5,1) | 5 | 10 | 2 | 10 | 10S1+2S2+10S3 |
(1,2,3) | 6 | ||||
…… | …… | …… | …… | …… | …… |
问题二:请将上面表格补充完整:当单位长方体的个数是6时,表面上面积为S1的个数是______.
表面上面积为S2的个数是______;表面上面积为S3的个数是______;表面积为______.
问题三:根据以上规律,请写出有序数组(x,y,z)的几何体表面积计算公式S(x,y,z)=______(用x、y、z、S1、S2、S3表示)
探究三:
同学们研究了当S1=2,S2=3,S3=4时,用3个单位长方体码放的几何体中,有三种码放的方法,有序数组分别为(1,1,3),(1,3,1),(3,1,1).而S(1,1,3)=38,S(1,3,1)=42,S(3,1,1)=46.容易发现个数相同的长方体,由于码放的方法不同,组成的几何体的表面积就不同.
拓展应用:
要将由20个相同的长方体码放的几何体进行打包,其中每个长方体的长是8,宽是5,高是6.为了节约外包装材料,请直接写出使几何体表面积最小的有序数组,并写出这个最小面积(不需要写解答过程).(缝隙不计)
【答案】(1)(1,2,3),6;(2)12,6,4,12S1+6S2+4S3;(3)2yzS1+2xzS2+2xyS3;拓展应用:几何体表面积最小的有序数组为(2,2,5),最小面积为S(2,2,5)=1786.
【解析】
(1)根据题中所给的标示法和图4中主视图知,摆放的长方体共有两列三层,由左视图知长方体共一排,则这种码放方式的有序数组为(1,2,3);组成这个几何体的单位长方体的个数为6个;
(2)几何体有序数组(1,2,3)时,表示几何体码放了1排2列3层,单位长方体的个数为6个,表面上面积为S1的个数为12个,表面上面积为S2的个数6个,表面上面积为S3的个数4个,表面积为:12S1+6S2+4S3;
(3)根据题意可知当有序数组(x,y,z)时,根据长方体的面积公式知,表面上面积为S1的个数为2yz个,表面上面积为S2的个数2xz个,表面上面积为S3的个数2xy个,该几何体表面积计算公式S(x,y,z)=2yzS1+2xzS2+2xyS3
(4)拓展应用:由题目中所给出的S1=2,S2=3,S3=4时,S(x,y,z)=2(yzS1+xzS2+xyS3)=2(2yz+3xz+4xy),分析出要使S(x,y,z)的值最小,应满足x≤y≤z(x、y、z为正整数),然后按条件将20分为:20=1×1×20、20=1×2×10、20=1×4×5、20=2×2×5四种形式,从面得出S(2,2,5)的值最小值为1786.
解:(1)根据如图4中主视图知,摆放的长方体共有两列三层,由左视图知长方体共一排,根据题中所给的标示法,则这种码放方式的有序数组为(1,2,3);
组成这个几何体的单位长方体的个数为1×2×3=6(个)
故答案 (1,2,3),6
(2)由题意知,当几何体有序数组(1,2,3)时,表示几何体码放了1排2列3层,单位长方体的个数为6个
∴表面上面积为S1的个数为12个,表面上面积为S2的个数6个,表面上面积为S3的个数4个,表面积为:12S1+6S2+4S3
故答案为:12,6,4,12S1+6S2+4S3;
(3)当有序数组(x,y,z)时,
表面上面积为S1的个数为2yz个,表面上面积为S2的个数2xz个,表面上面积为S3的个数2xy个,
∴该几何体表面积计算公式S(x,y,z)=2yzS1+2xzS2+2xyS3
故答案2yzS1+2xzS2+2xyS3
拓展应用:
当S1=2,S2=3,S3=4时,S(x,y,z)=2(yzS1+xzS2+xyS3)=2(2yz+3xz+4xy)
要使S(x,y,z)的值最小,不难看出x,y,z应满足x≤y≤z(x、y、z为正整数)
∵将相邻三个面的面积记为S1、S2、S3,且S1<S2<S3,其中每个长方体的长是8,宽是5,高是6
∴S1=30,S2=40,S3=48
∴满足要求的组合有(1,1,20),(1,2,10),(1,4,5),(2,2,5)
∵S(1,1,20)=2×30×20+2×40×20+2×48=2896
S(1,2,10)=2×30×2×10+2×40×10+2×48×2=2192
S(1,4,5)=2×30×4×5+2×40×5+2×48×4=1984
S(2,2,5)=2×30×2×5+2×40×2×5+2×48×4=1786
∴S(2,2,5)的值最小
∴几何体表面积最小的有序数组为(2,2,5),最小面积为S(2,2,5)=1786.


科目:初中数学 来源: 题型:
【题目】两位同学在足球场上游戏,两人的运动路线如图1所示,其中AC=DB,小王从点A出发沿线段AB运动到点B,小林从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示,结合图象分析,下列说法正确的是( )
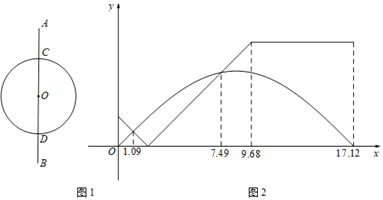
A. 小王的运动路程比小林的长
B. 两人分别在![]() 秒和
秒和![]() 秒的时刻相遇
秒的时刻相遇
C. 当小王运动到点D的时候,小林已经过了点D
D. 在![]() 秒时,两人的距离正好等于
秒时,两人的距离正好等于![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①![]() ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
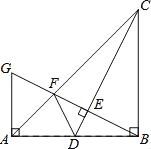
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】厨师将一定质量的面团做成粗细一致的拉面时,面条的总长度y(m)与面条横截面积x(mm2)之间成反比例函数关系.其图象经过A(4,32)、B(t,80)两点.
(1)求y与x之间的函数表达式;
(2)求t的值,并解释t的实际意义;
(3)如果厨师做出的面条横截面面积不超过3.2mm2,那么面条的总长度至少为_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时甲同学先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由乙同学从中随机抽取一张卡片,甲、乙两同学按各自抽取的内容进行诵读比赛.
请用列表或画树状图的方法求甲、乙两同学诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
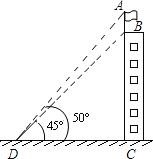
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com