
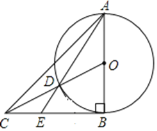
【题目】如图,AB=BC=2,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,则BE的长为______.
【答案】![]() -1
-1
【解析】
先根据已知和勾股定理得出CD的长,再根据直径所对的圆周角为直角和等腰三角形的性质证得∠CDE=∠CBD,然后根据两角对应相等两三角形相似得出△CDE∽△CBD,可得比例式,从而得到CD2=CECB,求得CE即可解决问题.
解:连接BD.
∵∠CBO=90°,BC=2,OB=1,
∴OC=![]() ,
,
∴CD=OC-OD=![]() -1,
-1,
∵AB是直径,
∴∠ADB=∠EDB=90°,
∴∠CDE+∠ODB=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∵∠CBD+∠OBD=90°,
∴∠CDE=∠CBD,
∵∠DCE=∠BCD,
∴△CDE∽△CBD,
∴CD2=CECB,
∴CE=3-![]() ,
,
∴BE=BC-CE=![]() -1.
-1.
故答案为![]() -1.
-1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
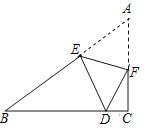
【题目】如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E、F分别在边AB、AC上,将△AEF沿直线EF折叠,使点A的对应点D恰好落在边BC上.若△BDE是直角三角形,则CF的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
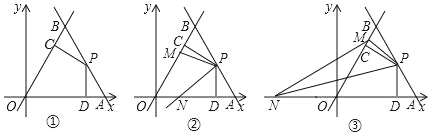
【题目】如图①,直线y=﹣![]() x+8
x+8![]() 与x轴交于点A,与直线y=
与x轴交于点A,与直线y=![]() x交于点B,点P为AB边的中点,作PC⊥OB与点C,PD⊥OA于点D.
x交于点B,点P为AB边的中点,作PC⊥OB与点C,PD⊥OA于点D.
(1)填空:点A坐标为 ,点B的坐标为 ,∠CPD度数为 ;
(2)如图②,若点M为线段OB上的一动点,将直线PM绕点P按逆时针方向旋转,旋转角与∠AOB相等,旋转后的直线与x轴交于点N,试求MBAN的值;
(3)在(2)的条件下,当MB<2时(如图③),试证明:MN=DN﹣MC;
(4)在(3)的条件下,设MB=t,MN=s,直接写出s与t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:求n个相同的长方体(相邻面的面积不相同)摆放成一个大长方体的表面积.
问题探究:探究一:
为了研究这个问题,同学们建立了如下的空间直角坐标系:空间任意选定一点O,以点O为端点,作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴,统称为坐标轴,它们的方向分别为ox(水平向前)、oy(水平向右)、oz(竖直向上)方向.
将相邻三个面的面积记为S1、S2、S3,且S1<S2<S3的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体S1所在的面与x轴垂直,S2所在的面与y轴垂直,S3所在的面与z轴垂直,如图1所示.
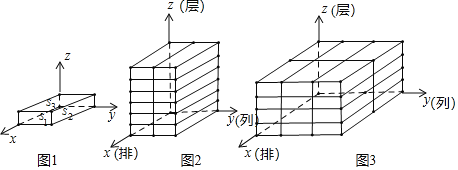
若将x轴方向表示的量称为几何体码放的排数,y轴方向表示的量称为几何体码放的列数,z轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标系内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作(1,2,6),如图3的几何体码放了2排3列4层,用有序数组记作(2,3,4).这样我们就可用每一个有序数组(x,y,z)表示一种几何体的码放方式.
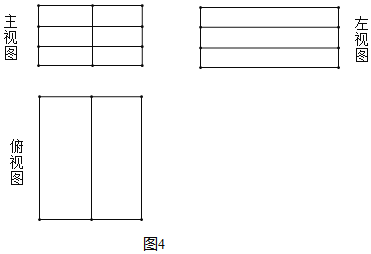
问题一:如图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为______.
组成这个几何体的单位长方体的个数为______个.
探究二:
为了探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),同学们针对若干个单位长方体进行码
放,制作了下列表格
几何体 有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
(1,1,1) | 1 | 2 | 2 | 2 | 2S1+2S2+2S3 |
(1,2,1) | 2 | 4 | 2 | 4 | 4S1+2S2+4S3 |
(3,1,1) | 3 | 2 | 6 | 6 | 2S1+6S2+6S3 |
(2,1,2) | 4 | 4 | 8 | 4 | 4S1+8S2+4S3 |
(1,5,1) | 5 | 10 | 2 | 10 | 10S1+2S2+10S3 |
(1,2,3) | 6 | ||||
…… | …… | …… | …… | …… | …… |
问题二:请将上面表格补充完整:当单位长方体的个数是6时,表面上面积为S1的个数是______.
表面上面积为S2的个数是______;表面上面积为S3的个数是______;表面积为______.
问题三:根据以上规律,请写出有序数组(x,y,z)的几何体表面积计算公式S(x,y,z)=______(用x、y、z、S1、S2、S3表示)
探究三:
同学们研究了当S1=2,S2=3,S3=4时,用3个单位长方体码放的几何体中,有三种码放的方法,有序数组分别为(1,1,3),(1,3,1),(3,1,1).而S(1,1,3)=38,S(1,3,1)=42,S(3,1,1)=46.容易发现个数相同的长方体,由于码放的方法不同,组成的几何体的表面积就不同.
拓展应用:
要将由20个相同的长方体码放的几何体进行打包,其中每个长方体的长是8,宽是5,高是6.为了节约外包装材料,请直接写出使几何体表面积最小的有序数组,并写出这个最小面积(不需要写解答过程).(缝隙不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
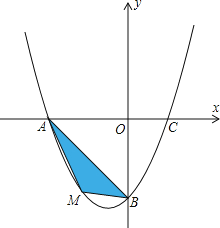
【题目】在平面直角坐标系中,已知抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点M为第三象限内抛物线上一动点,点M的横坐标为m,
若点M为第三象限内抛物线上一动点,点M的横坐标为m,![]() 的面积为S.求S关于m的函数关系式,并求出S的最大值.
的面积为S.求S关于m的函数关系式,并求出S的最大值.
![]() 若点P是抛物线上的动点,点Q是直线
若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
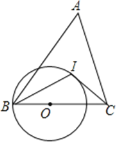
【题目】如图,△ABC中,AC=BC,点I是△ABC的内心,点O在边BC上,以点O为圆心,OB长为半径的圆恰好经过点I,连接CI,BI.
(1)求证:CI是⊙O的切线;
(2)若AC=BC=5,AB=6,求BI的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
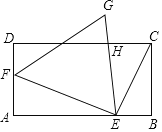
【题目】如图,已知矩形ABCD中,BC=2cm,AB=2![]() cm,点E在边AB上,点F在边AD上,点E由A向B运动,连结EC、EF,在运动的过程中,始终保持EC⊥EF,△EFG为等边三角形.
cm,点E在边AB上,点F在边AD上,点E由A向B运动,连结EC、EF,在运动的过程中,始终保持EC⊥EF,△EFG为等边三角形.
(1)求证△AEF∽△BCE;
(2)设BE的长为xcm,AF的长为ycm,求y与x的函数关系式,并写出线段AF长的范围;
(3)若点H是EG的中点,试说明A、E、H、F四点在同一个圆上,并求在点E由A到B运动过程中,点H移动的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
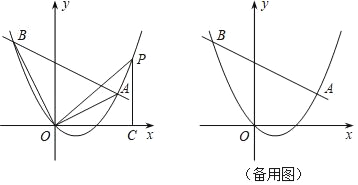
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
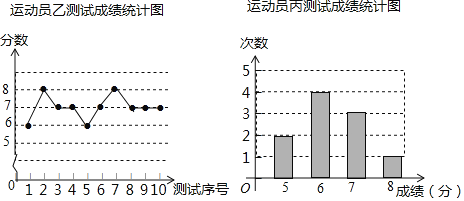
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com