
【题目】如图①,直线y=﹣![]() x+8
x+8![]() 与x轴交于点A,与直线y=
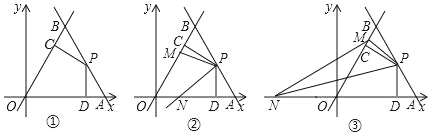
与x轴交于点A,与直线y=![]() x交于点B,点P为AB边的中点,作PC⊥OB与点C,PD⊥OA于点D.
x交于点B,点P为AB边的中点,作PC⊥OB与点C,PD⊥OA于点D.
(1)填空:点A坐标为 ,点B的坐标为 ,∠CPD度数为 ;
(2)如图②,若点M为线段OB上的一动点,将直线PM绕点P按逆时针方向旋转,旋转角与∠AOB相等,旋转后的直线与x轴交于点N,试求MBAN的值;
(3)在(2)的条件下,当MB<2时(如图③),试证明:MN=DN﹣MC;
(4)在(3)的条件下,设MB=t,MN=s,直接写出s与t的函数表达式.
【答案】(1)(8,0),(4,4![]() ),120°.(2)16;(3)证明见解析;(4)S=
),120°.(2)16;(3)证明见解析;(4)S=![]() +t﹣4(0<t<2).
+t﹣4(0<t<2).
【解析】分析:(1)利用待定系数法可得A、B两点坐标,根据tan∠BOA=![]() ,可得∠BOA=60°,再根据四边形内角和定理可求∠CPD;
,可得∠BOA=60°,再根据四边形内角和定理可求∠CPD;
(2)只要证明△PAN∽△MBP,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(3)如图③中,在DO上截取DK=MC,连接OP.只要证明△PCM≌△PDK,△PNM≌△PNK即可解决问题;
(4)利用(2)(3)中的结论即可解决问题;
详解:(1)如图①中,
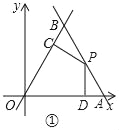
对于直线y=﹣![]() x+8
x+8![]() ,令y=0,解得x=8,可得A(8,0),
,令y=0,解得x=8,可得A(8,0),
由![]() ,解得
,解得![]() ,
,
∴B(4,4![]() ),
),
∴tan∠BOA=![]() ,
,
∴∠BOA=60°,
∵PC⊥OB与点C,PD⊥OA于点D,
∴∠PCO=∠PDO=90°,
∴∠CPD=120°,
故答案为(8,0),(4,4![]() ),120°.
),120°.
(2)如图②中,
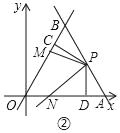
∵OA=OB=8,∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=8,∠OBA=∠OAB=60°,
∴PA=PB=4,
∵∠APM=∠APN+∠MPN=∠PMB+∠PBM,
∵∠MPN=∠PBM=60°,
∴∠APN=∠PMB,
∴△PAN∽△MBP,
∴![]() ,
,
∴MBAN=4×4=16.
(3)如图③中,在DO上截取DK=MC,连接OP.
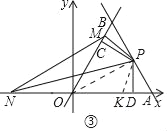
∵OB=OA,PB=PA,
∴∠POB=∠POA,
∵PC⊥OB与点C,PD⊥OA于点D,
∴PC=PD,∵∠PCM=∠PDK=90°,MC=DK,
∴△PCM≌△PDK,
∴PM=PK,∠CPM=∠DPK,
∴∠MPK=∠CPD=120°,
∵∠MPN=60°,
∴∠MPN=∠KPN=60°,∵PN=PN,
∴△PNM≌△PNK,
∴MN=KN=DN﹣DK=DN﹣CM.
(4)如图③中,由(2)可知:AN=![]() ,易知BC=AD=2,
,易知BC=AD=2,
∵MN=DN﹣CM,
∴MN=(AN﹣AD)﹣(BC﹣BM),
∴S=![]() ﹣2﹣(2﹣t)=
﹣2﹣(2﹣t)=![]() +t﹣4(0<t<2).
+t﹣4(0<t<2).


科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣kx+k2+n=0有两个不相等的实数根x1、x2,且(2x1+x2)2﹣8(2x1+x2)+15=0.
(1)求证:n<0;
(2)试用k的代数式表示x1;
(3)当n=﹣3时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
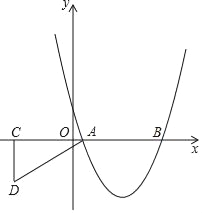
【题目】如图,抛物线y=x2+bx+c与x轴分别交于A(1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)过点C(﹣3,0)在x轴下方作x轴的垂线,再以点A为圆心、5为半径长画弧,交先前所作垂线于D,连接AD(如图),将Rt△ACD沿x轴向右平移m个单位,当点D落在抛物线上时,求m的值;
(3)在(2)的条件下,当点D第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(-3)-(-2)+(-4)
(2)(-![]() )-(-
)-(-![]() )-|-
)-|-![]() |-(-
|-(-![]() )
)
(3)-23÷![]() ×(-
×(-![]() )2
)2
(4)(![]() )×(-36)
)×(-36)
(5)-14-![]() ×
×![]()
(6)(-1)4+5÷(-![]() )×(-6)
)×(-6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB//CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合).![]() ,
,![]() .
.
(1)若点B在点A的左侧,求∠BED的度数(用含![]() 的代数式表示).
的代数式表示).
(2)将线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断![]() 的度数是否改变.若改变,请求出
的度数是否改变.若改变,请求出![]() 的度数(用含
的度数(用含![]() 的代数式表示);若不变,请说明理由.
的代数式表示);若不变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:

请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com