
،¾جâؤ؟،؟س؟بھصٍتاضذ¹ْخق؛ثأغ½غض®د磬زرضھؤ³أغ½غضضض²´َ»§·ë´َز¯µؤأغ½غ³ة±¾خھ2شھ/ا§؟ث£¬بç¹ûشعخ´ہ´90جىأغ½غµؤدْتغµ¥¼غp£¨شھ/ا§؟ث£©سëت±¼نt£¨جى£©ض®¼نµؤ؛¯ت¹طدµت½خھp=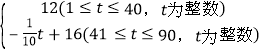 £¬ازأغ½غµؤبصدْء؟y£¨ا§؟ث£©سëت±¼نt£¨جى£©آْ×مز»´خ؛¯ت¹طدµ£¬ئن²؟·ضت¾فبçدآ±يثùت¾£؛
£¬ازأغ½غµؤبصدْء؟y£¨ا§؟ث£©سëت±¼نt£¨جى£©آْ×مز»´خ؛¯ت¹طدµ£¬ئن²؟·ضت¾فبçدآ±يثùت¾£؛
ت±¼نt/جى | 1 | 10 | 20 | 40 | 70 | 90 |
بصدْتغء؟y/ا§؟ث | 105 | 150 | 200 | 300 | 450 | 550 |
£¨1£©اَyسëtض®¼نµؤ؛¯ت±ي´ïت½£»
£¨2£©شعخ´ہ´90جىµؤدْتغضذ£¬ش¤²âؤؤز»جىµؤبصدْتغہûبَ×î´َ£؟×î´َبصدْتغہûبَخھ¶àةظشھ£؟
£¨3£©شعتµ¼تدْتغµؤ؛َ50جىضذ£¬·ë´َز¯¾ِ¶¨أ؟دْتغ1ا§؟ثأغ½غ¾ح¾èشùnشھہûبَ£¨n£¼5£©¸ّءôتط¶ùح¯×÷خھضْر§½ً£¬دْتغ¹³جضذ·ë´َز¯·¢دض£¬ا،؛أ´سµع51جى؟ھت¼£¬؛حا°ز»جىدà±ب£¬؟غ³¾èشù؛َµؤبصدْتغہûبَضًبص¼ُةظ£¬اëاَ³ِnµؤب،ضµ·¶خ§£®
،¾´ً°¸،؟£¨1£©y=5t+100£»£¨2£©ا°60جىہûبَ×î´َ£¬×î´َہûبَخھ3200شھ£»£¨3£©nµؤب،ضµ·¶خ§خھ1.9،ـn£¼5£®
،¾½âخِ،؟
£¨1£©شثسأ´¶¨دµت·¨اَ³ِ؛¯ت½âخِت½£»£¨2£©ةèµعxجىµؤدْتغہûبَخھwشھ£®µ±1،ـt،ـ40ت±£¬سةجâزâw=£¨12-2£©£¨5t+100£©=50t+1000£»µ±t=40ت±w×î´َضµخھ3000شھ£»µ±41،ـt،ـ90ت±£¬w=£¨5t+100£©£¨-![]() t+16-2£©=-
t+16-2£©=-![]() t2+60t+1400£¬شظاَ؛¯ت×îضµ£»£¨3£©ةèأ؟جى؟غ³¾èشù؛َµؤبصدْتغہûبَخھmشھ£®سةجâزâm=£¨5t+100£©£¨-
t2+60t+1400£¬شظاَ؛¯ت×îضµ£»£¨3£©ةèأ؟جى؟غ³¾èشù؛َµؤبصدْتغہûبَخھmشھ£®سةجâزâm=£¨5t+100£©£¨-![]() t+16-2£©-£¨5t+100£©n=-
t+16-2£©-£¨5t+100£©n=-![]() t2+£¨60-5n£©t+1400-100n£¬¸ù¾فتµ¼تµأ49.5،ـ60-5n£¼50.5£¬1.9£¼n،ـ2.1£¬؟ة½ّز»²½اَ³ِnµؤب،ضµ·¶خ§.
t2+£¨60-5n£©t+1400-100n£¬¸ù¾فتµ¼تµأ49.5،ـ60-5n£¼50.5£¬1.9£¼n،ـ2.1£¬؟ة½ّز»²½اَ³ِnµؤب،ضµ·¶خ§.
½â£؛£¨1£©ةèy=kt+b£¬°رt=1£¬y=105£»t=10£¬y=150´ْبëµأµ½£؛![]() £¬
£¬
½âµأ£؛![]() £¬
£¬
،ày=5t+100£»
£¨2£©ةèµعxجىµؤدْتغہûبَخھwشھ£®
µ±1،ـt،ـ40ت±£¬سةجâزâw=£¨12-2£©£¨5t+100£©=50t+1000£»
µ±t=40ت±w×î´َضµخھ3000شھ£»
µ±41،ـt،ـ90ت±£¬w=£¨5t+100£©£¨-![]() t+16-2£©=-
t+16-2£©=-![]() t2+60t+1400£¬
t2+60t+1400£¬
،ك¶ش³ئضلt=60£¬a=-![]() £¼0£¬
£¼0£¬
،àشع¶ش³ئضل×َ²àwثوxشِ´َ¶ّشِ´َ£¬
،àt=60ت±£¬w×î´َضµ=3200£¬
×غةدثùتِا°60جىہûبَ×î´َ£¬×î´َہûبَخھ3200شھ£®
£¨3£©ةèأ؟جى؟غ³¾èشù؛َµؤبصدْتغہûبَخھmشھ£®
سةجâزâm=£¨5t+100£©£¨-![]() t+16-2£©-£¨5t+100£©n=-
t+16-2£©-£¨5t+100£©n=-![]() t2+£¨60-5n£©t+1400-100n£¬
t2+£¨60-5n£©t+1400-100n£¬
،كشع؛َ50جىضذ£¬أ؟جى؟غ³¾èشù؛َµؤبصدْتغہûبَثوت±¼نtµؤشِ´َ¶ّ¼ُةظ£¬
،à49.5،ـ60-5n£¼50.5£¬
،à1.9£¼n،ـ2.1£®
سض،كn£¼5£¬
،ànµؤب،ضµ·¶خ§خھ1.9،ـn£¼5£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ABخھ،رOµؤض±¾¶£¬دزCD،حAB£¬´¹×مخھµمP£¬ض±دكBFسëADµؤرس³¤دك½»سعµمF£¬از،دAFB=،دABC£®
(1)اَض¤£؛ض±دكBFتا،رOµؤاذدك£®
(2)بôCD=2![]() £¬OP=1£¬اَدك¶خBFµؤ³¤£®
£¬OP=1£¬اَدك¶خBFµؤ³¤£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼ثùت¾,½«¾طذخOABCضأسعئ½أوض±½ا×ّ±êدµضذ,µمA,C·ض±ًشعx,yضلµؤص°ëضلةد,زرضھµمB(4,2),½«¾طذخOABC·صغ,ت¹µأµمCµؤ¶شس¦µمPا،؛أآنشعدك¶خOA(°üہ¨¶ثµمO,A)ةد,صغ؛غثùشعض±دك·ض±ً½»BC،¢OAسعµمD،¢E£»بôµمPشعدك¶خOAةدشث¶¯ت±,¹µمP×÷OAµؤ´¹دك½»صغ؛غثùشعض±دكسعµمQ.
£¨1£©اَض¤£؛CQ=QP
£¨2£©ةèµمQµؤ×ّ±êخھ(x,y),اَy¹طسعxµؤ؛¯ت¹طدµت½¼°×ش±نء؟xµؤب،ضµ·¶خ§;
£¨3£©بçح¼2,ء¬½لOQ,OB,µ±µمPشعدك¶خOAةدشث¶¯ت±,ةèب½اذخOBQµؤأو»خھS,µ±xب،؛خضµت±,Sب،µأ×îذ،ضµ,²¢اَ³ِ×îذ،ضµ£»
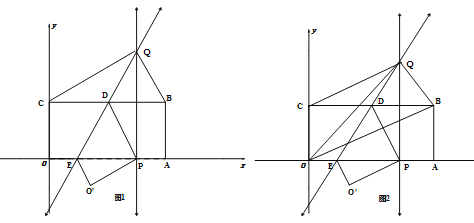
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
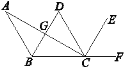
،¾جâؤ؟،؟بçح¼£¬AB،خCD£¬BDئ½·ض،دABC£¬CEئ½·ض،دDCF£¬،دACE£½90،م.
(1)إذ¶دBD؛حCEµؤخ»ضأ¹طدµ£¬²¢ثµأ÷ہيسة£»
(2)إذ¶دAC؛حBDتا·ٌ´¹ض±£¬²¢ثµأ÷ہيسة£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
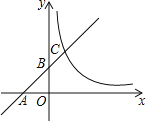
،¾جâؤ؟،؟بçح¼£¬![]() £¨bخھ³£ت£©µؤح¼دَسëxضل£¬yضل·ض±ً½»سعµمA£¬Bسë·´±بہ؛¯ت
£¨bخھ³£ت£©µؤح¼دَسëxضل£¬yضل·ض±ً½»سعµمA£¬Bسë·´±بہ؛¯ت![]() £¨x£¾0£©µؤح¼دَ½»سعµمC£®بôACBC£½4£¬شٍkµؤضµخھ_____£®
£¨x£¾0£©µؤح¼دَ½»سعµمC£®بôACBC£½4£¬شٍkµؤضµخھ_____£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
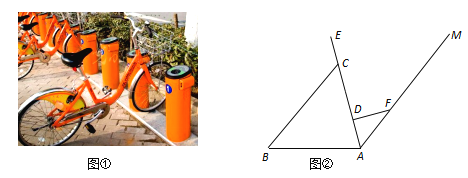
،¾جâؤ؟،؟،°µحج¼»·±££¬ؤمخزح¬ذذ،±£®½ü¼¸ؤ꣬¸÷´َ³اتذµؤ¹«¹²×شذذ³µ¸ّتذأٌ³ِذذ´ّہ´ءث¼«´َµؤ·½±م£®ح¼¢ظتا¹«¹²×شذذ³µµؤتµخïح¼£¬ح¼¢عتا¹«¹²×شذذ³µµؤ³µ¼ـت¾زâح¼£¬µمA£®D،¢C،¢Eشعح¬ز»جُض±دكةد£¬CD=30cm£¬DF=20cm£¬AF=25cm£¬FD،حAEسعµمD£¬×ù¸ثCE=15cm£¬از،دEAB=75،م£®
£¨1£©اَADµؤ³¤£»
£¨2£©اَµمEµ½ABµؤ¾àہ룮£¨²خ؟¼ت¾ف£؛sin75،م،ض0.97£¬cos75،م،ض0.26£¬tan75،م،ض3.73£©
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
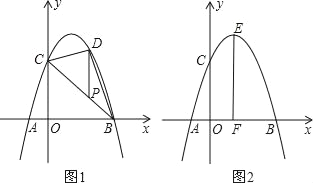
،¾جâؤ؟،؟إ×خïدكy=©پx2+bx+c¾¹µمA،¢B،¢C£¬زرضھA£¨©پ1£¬0£©£¬C£¨0£¬3£©£®
£¨1£©اَإ×خïدكµؤ½âخِت½£»
£¨2£©بçح¼1£¬Pخھدك¶خBCةدز»µم£¬¹µمP×÷yضلئ½ذذدك£¬½»إ×خïدكسعµمD£¬µ±،÷BDCµؤأو»×î´َت±£¬اَµمPµؤ×ّ±ê£»
£¨3£©بçح¼2£¬إ×خïدك¶¥µمخھE£¬EF،حxضلسعFµم£¬M£¨m£¬0£©تاxضلةدز»¶¯µم£¬Nتادك¶خEFةدز»µم£¬بô،دMNC=90،م£¬اëض¸³ِتµتmµؤ±ن»¯·¶خ§£¬²¢ثµأ÷ہيسة£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
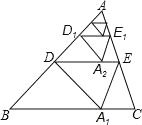
،¾جâؤ؟،؟بçح¼£¬½«،÷ABCرط×إ¹APضذµمDµؤض±دكصغµ£¬ت¹µمAآنشعB C±كةدµؤA1´¦£¬³ئخھµع1´خ²ظ×÷£¬صغ؛غDEµ½BCµؤ¾àہë¼اخھh1£¬»¹شض½ئ¬؛َ£¬شظ½«،÷ADEرط×إ¹ADضذµمD1µؤض±دكصغµ£¬ت¹µمAآنشعDE±كةدµؤA2´¦£¬³ئخھµع2´خ²ظ×÷£¬صغ؛غD1E1µ½BCµؤ¾àہë¼اخھh2£¬°´ةدتِ·½·¨²»¶د²ظ×÷دآب¥،¾¹µع2018´خ²ظ×÷؛َµأµ½µؤصغ؛غD2017E2017µ½BCµؤ¾àہë¼اخھh2018£¬بôh1=1£¬شٍh2018µؤضµخھ£¨،،،،£©
A. 2©پ![]() B.
B. ![]() C. 1©پ
C. 1©پ![]() D. 2©پ
D. 2©پ![]()
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ABتا،رOµؤض±¾¶£¬µمEتا»،BFµؤضذµم£¬ء¬½سAF½»¹EµؤاذدكسعµمD£¬ABµؤرس³¤دك½»¸أاذدكسعµمC£¬بô،دC£½30،م£¬،رOµؤ°ë¾¶تا2£¬شٍح¼ذخضذزُس°²؟·ضµؤأو»تا_____£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com