
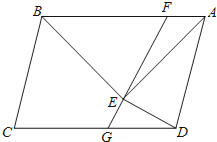
【题目】如图:已知ABCD中,以AB为斜边在ABCD内作等腰直角△ABE,且AE=AD,连接DE,过E作EF⊥DE交AB于F交DC于G,且∠AEF=15°
(1)若EF=![]() ,求AB的长.
,求AB的长.
(2)求证:2GE+EF=AB.
【答案】(1)AB=3;(2)见解析
【解析】
试题分析:(1)作EH⊥AB,交AB于H,根据等腰直角三角形的性质得到∠EAB=∠EBA=45°,EA=EB,于是得到EH=HB=AH=![]() AB,于是得到∠EFH=∠EAB+∠AEF=60°,求得∠FEH=30°,根据直角三角形的性质即可得到结论;
AB,于是得到∠EFH=∠EAB+∠AEF=60°,求得∠FEH=30°,根据直角三角形的性质即可得到结论;
(2)连接EC,根据三角形的内角和得到∠DEA=∠EDA=75°,于是得到∠EAD=30°,求出∠DAB=∠DCB=75°,∠CBA=∠CDA=105°,由于∠ABE=45°,得到∠CBE=60°,推出△BCE是等边三角形,求出∠DCE=15°,CE=BE=AE,推出DG=2GE,证得△AEF≌△ECG,根据全等三角形的性质得到GC=FE,即可得到结论.
解:(1)作EH⊥AB,交AB于H,
∵△ABE是等腰直角三角形,
∴∠EAB=∠EBA=45°,EA=EB,
∴EH=HB=AH=![]() AB,
AB,
∴∠EFH=∠EAB+∠AEF=60°,
∴∠FEH=30°,
∴FH=![]() EF=
EF=![]() EH=
EH=![]() ,
,
∴AB=3,
(2)连接EC,
∵∠AEF=15°,EF⊥DE,AE=AD,
∴∠DEA=∠EDA=75°,
∴∠EAD=30°,
∵∠BAE=45°,
∴∠DAB=∠DCB=75°,∠CBA=∠CDA=105°,
∵∠ABE=45°,
∴∠CBE=60°,
∵AD=BE=BC,
∴△BCE是等边三角形,
∴∠DCE=15°,CE=BE=AE,
∵∠GED=90°,∠GDC=30°,∠DGE=60°,
∴DG=2GE,
∵∠EGC=105°=∠AFE,CE=EF,∠DCE=15°=∠AEF,
在△AEF与△ECG中, ,
,
∴△AEF≌△ECG,
∴GC=FE,
∴AB=DC=DG+GC=2GE+CG=2GE+EF.



科目:初中数学 来源: 题型:
【题目】已知,如图△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.
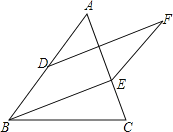
(1)猜想:DF与AE的关系是 ;
(2)试说明你猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是( )
A. 1米 B. 1.5米 C. 2米 D. 2.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四个三角形分别满足下列条件:①一个内角等于另两个内角之和;②三个内角度数之比为3∶4∶5;③三边长分别为7,24,25;④三边长之比为5∶12∶13.其中直角三角形有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2-8x-1=0配方后可变形为( )
A. (x+4)2=17 B. (x+4)2=15 C. (x-4)2=17 D. (x-4)2=15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com