
分析 将题目中的各个方程化为一般形式,然后根据△的值,判断方程的根的情况,然后根据根与系数的关系可以求得方程的两根之和与两根之积.
解答 解:(1)x2-3x-1=0
∵a=1,b=-3,c=-1,
∴△=b2-4ac=(-3)2-4×1×(-1)=13>0.
∴方程有两个不等的实数根.
∴${x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{-3}{1}=3$,${x}_{1}{x}_{2}=\frac{c}{a}=\frac{-1}{1}=-1$.
(2)(x-2)(2x-1)=5
化简,得 2x2-5x-3=0.
∵a=2,b=-5,c=-3,
∴△=b2-4ac=(-5)2-4×2×(-3)=49>0.
∴方程有两个不等的实数根.
∴${x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{-5}{2}=\frac{5}{2}$,${x}_{1}{x}_{2}=\frac{c}{a}=\frac{-3}{2}=-\frac{3}{2}$.
(3)(2x-1)2=3x
化简,得 4x2-7x+1=0.
∵a=4,b=-7,c=1,
∴△=b2-4ac=(-7)2-4×4×1=33>0.
∴方程有两个不等的实数根.
∴${x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{-7}{4}=\frac{7}{4}$,${x}_{1}{x}_{2}=\frac{c}{a}=\frac{1}{4}$.
(4)$\frac{2x^{2}-5x}{4}$=$\frac{x+1}{2}$
化简,得 2x2-7x-2=0.
∵a=2,b=-7,c=-2,
∴△=b2-4ac=(-7)2-4×2×(-2)=65>0.
∴方程有两个不等的实数根.
∴${x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{-7}{2}=\frac{7}{2}$,${x}_{1}{x}_{2}=\frac{c}{a}=\frac{-2}{2}=-1$.
点评 本题考查根的判别式、根与系数的关系,关键是将方程进行化简,化为一般形式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
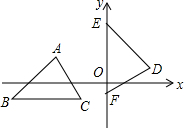 如图,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F.若A点的坐标分别为(-5,3),B,C点的纵坐标都为-3,E,F点在y轴上,D点在第一象限,则D点的横坐标为6.
如图,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F.若A点的坐标分别为(-5,3),B,C点的纵坐标都为-3,E,F点在y轴上,D点在第一象限,则D点的横坐标为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com