
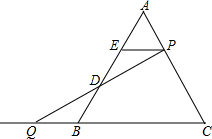
 如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.
如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.分析 (1)根据平行线的性质,可得∠AEP=∠ABC,∠EPD=∠Q,根据全等三角形的判定与性质,可得答案;
(2)根据等腰三角形的性质,证得PE=BQ,由直角三角形的性质得到PC=$\frac{1}{2}$CQ,根据线段的和差,可得答案.
解答 证明:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵PE∥BC,
∴∠AEP=∠APE=∠ABC=∠ACB=60°,
∴AP=PE,
∵AP=BQ,
∴PE=BQ,
∵PE∥BQ,
∴∠EPD=∠DQB,∠PED=∠QBD,
在△PED与△QBD中,$\left\{\begin{array}{l}{∠EPD=∠DQB}\\{PE=BQ}\\{∠PED=∠QBD}\end{array}\right.$,
∴△PED≌△QBD;
(2)∵PQ⊥AC,∠C=60°,
∴∠PQC=30°,
∴PC=$\frac{1}{2}$CQ,
由(1)证得PE=BQ,
∴AC-AP=BC-PE=$\frac{1}{2}$(PE+BC),
∴BC-PE=$\frac{1}{2}$FE$+\frac{1}{2}$BC,
∴$PE=\frac{1}{3}$BC,
∴$PE=\frac{1}{4}$CQ.
点评 题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,线段中点的性质,能证得PC=$\frac{1}{2}$CQ是解题的关键.


科目:初中数学 来源: 题型:解答题
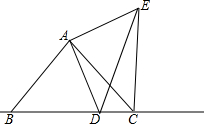 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11.64亿 | B. | 11.64×108亿 | C. | 1.164×109亿 | D. | 116.4×107亿 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
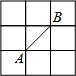 如图所示的正方形网格中,网格线的交点称为格点,已知A、B 两点为格点,如果C也是图中的格点,则满足△ABC为等腰三角形的点C的个数为( )
如图所示的正方形网格中,网格线的交点称为格点,已知A、B 两点为格点,如果C也是图中的格点,则满足△ABC为等腰三角形的点C的个数为( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
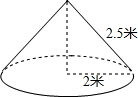 一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).
一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).| A. | $\frac{25}{4}$π | B. | 5π | C. | 4π | D. | 3π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com