
分析 首先根据幂的乘方的运算方法,分别求出a3x、a2y的值各是多少;然后根据同底数幂的除法的运算方法,求出算式a3x-2y的值是多少即可.
解答 解:∵ax=3,
∴a3x=(ax)3=33=27,
∵ay=5,
∴a2y=(ay)2=52=25,
∴a3x-2y=$\frac{{a}^{3x}}{{a}^{2y}}=\frac{27}{25}$.
故答案为:$\frac{27}{25}$.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的除法法则:同底数幂相除,底数不变,指数相减,要熟练掌握,解答此题的关键是要明确:①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
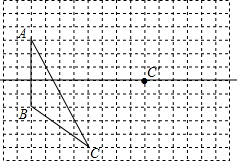 画图并填空:如图,方格纸中每个小正方形的边长都为1.
画图并填空:如图,方格纸中每个小正方形的边长都为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元.
如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:
如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形OABC,A(0,5),C(4,0),正比例函数y=mx(m≠0)的图象经过点B.
如图,矩形OABC,A(0,5),C(4,0),正比例函数y=mx(m≠0)的图象经过点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com